（１） 感度 と 特異度

　陰陽検査とは、あるものが ある集合（ 集合Ａとします ）に属するか否かを判定するものです。
　陰陽検査の感度とは、集合Ａに属するものを多数検査したとき、それが集合Ａに属するものだと間違いなく判定できる確率のことで、感度は集合Ａに属するものと属さないものが半々に存在する条件下で調査したときに、調査対象のものが集合Ａに属することを正しく判断する確率（ 陽性的中率 ）に大変近いです。
　陰陽検査の特異度とは、集合Ａに属さないものを多数検査したとき、それが集合Ａに属さないものだと間違いなく判定できる確率のことで、特異度は集合Ａに属するものと属さないものが半々に存在する条件下で調査したときに、調査対象のものが集合Ａに属さないことを正しく判断する確率（ 陰性的中率 ）に大変近いです。

　集合Ａに属するものが属さないものよりも圧倒的に多い状況下で無作為に選んだ１つのものに陰陽検査を試行すると、陽性的中率は感度よりもかなり高くなり、陰性的中率は特異度よりもかなり低くなります。逆に、集合Ａに属するものが属さないものよりも圧倒的に少ない状況下で無作為に選んだ１つのものに陰陽検査を試行すると、陽性的中率は感度よりもかなり低くなり、陰性的中率は特異度よりもかなり高くなります。

　だからといって、集合Ａに属するものと集合Ａに属さないものを同数用意しなければ感度と特異度を求めることができないのではありません。多数のものが集合Ａに属するか属さないのかが分かっていれば、陰陽検査の感度と特異度を求めることができます。

　陰陽検査 の感度(%) を a×100 、特異度(%)を b×100 として、検査結果を表にすると次のようになります。


		陰陽検査
		陽性	陰性	計
集合Ａ	属する	a n	(100−a) n	100 n
	非要素	(100−b) m	b m	100 m
	計	100 m＋a n−b m	100 n−a n ＋b m	100 n＋100 m


　　a n ÷ 100 n × 100　＝→　a　（ 感度 ）
　　b m ÷ 100 m × 100　＝→　b　（ 特異度 ）
　　a n ÷ ( 100 m＋a n−b m ) × 100　（ 陽性的中率 ）
　　b m ÷ ( 100 n−a n＋b m ) × 100　（ 陰性的中率 ）

　m ＝ n のとき：

		陰陽検査
		陽性	陰性	計
集合Ａ	属する	a n	(100−a) n	100 n
	非要素	(1−b) n	b n	100 n
	計	(100＋a−b) n	(100−a＋b) n	200 n


　　a n ÷ 100 n × 100　＝→　a　（ 感度 ）
　　b n ÷ 100 n × 100　＝→　b　（ 特異度 ）
　　a n ÷ {(100＋a−b) n } × 100　（ 陽性的中率 ）
　　b n ÷ {(100−a＋b) n } × 100　（ 陰性的中率 ）
　　　　b ＝ a のとき：
　　　　　　　陽性的中率 ＝ 感度　　　陰性的中率 ＝ 特異度

（２） 陽性的中率 と 陰性的中率

感染者率 n % の弱毒細菌について陰陽検査Ａを用いて感染者か非感染者の判定を行います。
陰陽検査Ａ は 感度が a % で 特異度が b % です。


		陰陽検査Ａ
		陽性	陰性	計
	感染者		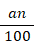	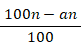n
	非感染		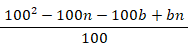	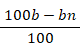100−n
	計		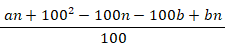	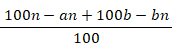100


　　　感染者だと判定された人のうち感染者である確率（ 陽性的中率（%））は、
　　　　　　
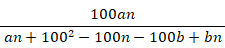
　　　非感染者だと判定された人のうち非感染者である確率（ 陰性的中率（%））は、
　　　　　　

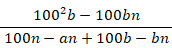
　　　　　　　　　※　偽陽性率（%）＝ 100−陽性的中率（%）
　　　　　　　　　　　偽陰性率（%）＝ 100−陰性的中率（%）

シミュレーション：
有病率： %
　　※ 有病率にも、国民有病率 とか 検査対象者内有病率とか あるので要注意です。
感 度 ： %
特異度： %

　　　

陽性的中率： %
陰性的中率： %



　※ 参照： JavaScript ＞ JavaScript＿算数 ＞ 陽性的中率