【 問 題 】

　5 cm × 5 cm × 100 cm の直方体の物質があります。質量は 10 kg で密度は均一で変形しません。
この直方体が横長く水平になるように２点で支えます。

　　（１）　左端から 20 cm の所（支点Ａ） と 右端から 20 cm の所（支点Ｂ） で支えた場合、
　　　　　それぞれの支点が直方体に作用する垂直抗力の大きさいくらでしょうか？

　　（２）　左端から 20 cm の所（支点Ａ） と 右端から 40 cm の所（支点Ｂ） で支えた場合、
　　　　　それぞれの支点が直方体に作用する垂直抗力の大きさいくらでしょうか？

　　　　　　　　　

【 解 答 】

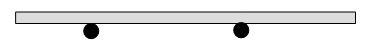
（１）　答えは、ＡもＢも 5g N （ g は重力加速度 ）、 合せて 10g N です。


最初に、支点Ａを中心とするトルク（ 力のモーメント ）のつり合いを考えます。
まず、物質にかかる重力によるトルクですが、
　　　　　　時計回りのトルクは、8g N × 0.4 m ＝→ 3.2g Nm
　　　　　　反時計回りのトルクは、2g N × 0.1 m ＝→ 0.2g Nm
次に、支点Ｂの垂直抗力による反時計回りのトルクが、F_B N × 0.6 m ＝→ 0.6 × F_B Nm
トルクのつり合いより、0.2g ＋ 0.6 × F_B ＝ 3.2g
よって、 F_B ＝ 5g

最後に、支点Ｂを中心とするトルクのつり合いを考えます。
　　　（ 省 略 ）



（２）　答えは、Ａは 2.5g N 、Ｂは 7.5g N、 合せて 10g N です。


最初に、支点Ａを中心とするトルクのつり合いを考えます。
まず、物質にかかる重力によるトルクですが、
　　　　　　時計回りのトルクは、8g N × 0.4 m ＝→ 3.2g Nm
　　　　　　反時計回りのトルクは、2g N × 0.1 m ＝→ 0.2g Nm
次に、支点Ｂの垂直抗力による反時計回りのトルクが、F_B N × 0.4 m ＝→ 0.4 × F_B Nm
トルクのつり合いより、0.2g ＋ 0.4 × F_B ＝ 3.2g
よって、 F_B ＝ 7.5g

最後に、支点Ｂを中心とするトルクのつり合いを考えます。
まず、物質にかかる重力によるトルクですが、
　　　　　　時計回りのトルクは、4g N × 0.2 m ＝→ 0.8g Nm
　　　　　　反時計回りのトルクは、6g N × 0.3 m ＝→ 1.8g Nm
次に、支点Ａの垂直抗力による時計回りのトルクが、F_A N × 0.4 m ＝→ 0.4 × F_A Nm
トルクのつり合いより、1.8g ＝ 0.8g＋ 0.4 × F_A
よって、 F_A ＝ 2.5g