放物線上の2点を通る直線
 図形の方程式 へ戻る
図形の方程式 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2021.12.30____
【 問 題 】
y = a x2 上の 2点 P( p, ap2 ) と Q( q, aq2 ) を結ぶ直線の方程式を求めよ
【 解 答 】
求める直線の方程式を y = m x + n とする。
この直線と放物線 y = a x2 の交点の x 座標を求めるには次の方程式を解けばいい。
a x2 = m x + n
つまり、
a x2 − m x − n = 0
この方程式の解が p と q となるためには、上式は次の式と同等でなければならない。
a ( x−p ) ( x−q ) = 0
つまり、
a x2 − a ( p+q ) x + apq = 0
以上の2つの式が同等になるための必要十分条件は、次の2つの式が成り立つことである。
a ( p+q ) = m
apq = −n
したがって、求める直線の方程式は次のようになる。
y = a ( p+q ) x − apq
【 別解法 】
2点 P(
P1, P2 ) と Q(
Q1,
Q2 ) を結ぶ直線の方程式
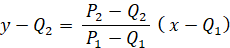
を用いても、y = a ( p+q ) x − apq を得ることができます。
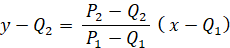
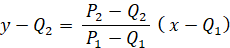
 図形の方程式 へ戻る
図形の方程式 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る