点Q と 点W から等しい距離にある点の集合は、 線分QWの垂直2等分線になることは有名です。 では、 点Wからの距離が点Qからの距離のP倍 ( ただし P > 1 ) になっている点の集合はどのようになるでしょうか?
求める点を ( x ,y ) で表すと、 次の式が成り立ちます。
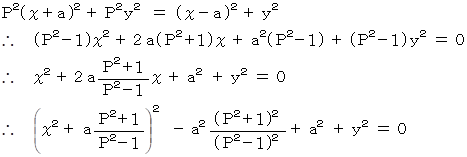
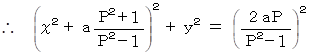
上記の式が求める答えになります。 これは円の方程式です。
-
たとえば、 P=2, a=9 のときは次のようになります。
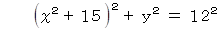
これは、 中心が( −15, 0 ) 半径が 12 の円です。
この円が x軸と交わる点は、 ( −27, 0 ) と ( −3, 0 ) です。
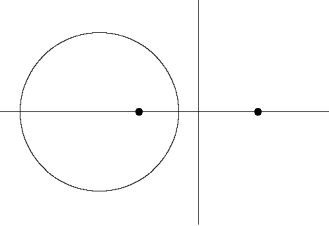
 図形の方程式 へ戻る
図形の方程式 へ戻る