点Ｑ（ ３，０ ） と　点Ｗ（ −３，０ ）があります。点Ｑ と 点Ｗ からの距離の和が 10 の点の集合はどんな図形になるでしょうか？

求める点を（ x，y ）で表すと、次の式が成り立ちます。
　　　
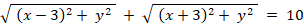
この式を順に変形していくと、次のようになります。
　　　
　　　
　　　
　　　
　　　
　　　
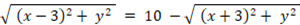
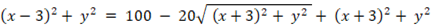
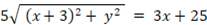
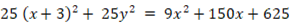
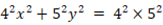
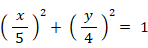
上式は楕円を表します。中心が原点にあって、長軸が x 軸上にあり長軸半径の長さが 5 、短軸が y 軸上にあり短軸半径の長さが 4 の楕円です。そして、点Ｑ と 点Ｗ を焦点とする楕円です。

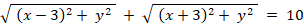
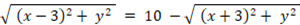
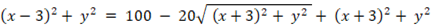
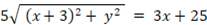
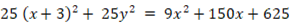
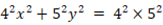
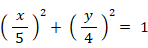
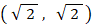　点Ｑ 　と　点Ｗ 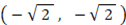　があります。点Ｑ と 点Ｗ からの距離の差が 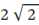で、点Ｗよりも点Ｑに近い点の集合はどんな図形になるでしょうか？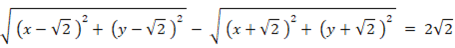

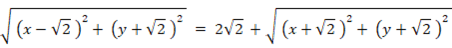
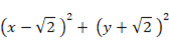
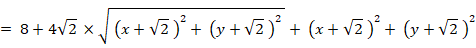
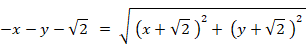
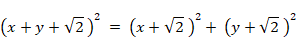
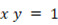
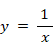求める点を（ x， y ）で表すと、次の式が成り立ちます。
　　　
この式を順に変形していくと、次のようになります。
　　　
　　　
　　　　　　　
　　　
　　　
　　　
　　　　　　ただし、x ＞ ０

上式は双曲線を表します。第一象限に存在する双曲線です。