平均値からの正負の記号付きの偏差を標準偏差で割った値を確率変数とし、標準偏差を 1 とする、 標準正規分布関数( 正確には「標準正規分布に従う確率変数 x の確率密度関数 f (x) 」と言います。)は、確率密度関数の代表です。今回は、そのルーツに迫りましょう。
(1) 2次元正規分布が作る確率密度曲面( 2次元正規分布曲面 )
-
無風下で25メール離れた的に向かって弓矢の名人が矢を放ちます。十万回施行します。的のどこに当たるかの確率分布を取ると、それは、的の中心を頂きとする体積1の山になり、その頂点を含む垂直断面の縁は1次元正規分布曲線に似たもの( 全範囲積分が1にならないので正規分布曲線とは言えません )になります。2次元正規分布曲面では的からの距離が等しい所は当たる確率密度が等しくなっています。そこで、的からの距離が等しい所はすべて的の中心を通る一つの直線上に当たったものとみなすことにします。すると、確率変数を2次元から1次元に落とし込むことができます。このとき、的からの距離( 正負の方向を含む )が確率変数になっています。そして、この曲線の高さを拡大縮小して全範囲積分が1になるようにしてやれば正規分布曲線になります。
-
的には、的の中止を原点とし、横軸を x 軸とし、縦軸を y 軸とする、座標系があるとします。
的を射たときに 直線 x = a2 上に当たる確率を f (a2) とします。
的を射たときに 直線 x = a2+b2 上に当たる確率は f (a2+b2) です。
的を射たときに 直線 y = b2 上に当たる確率を h (b2) とします。
的を射たときに 直線 y = 0 上に当たる確率は h (0) です。
(1)より次の式が成り立ちます。
h (0) × f (a2+b2) = f (a2) × h (b2)
的を90°時計回りに回転させると y 軸は x 軸 に重なるので、次の式が成り立つことがわかります。
h (b2) = f (b2)
したがって、次の式が成り立ちます。
f (0) × f (a2+b2) = f (a2) × f (b2)
したがって、次のことが分ります。
f (x) = c × (e k ) x2
h (0) × f (a2+b2) = f (a2) × h (b2)
的を90°時計回りに回転させると y 軸は x 軸 に重なるので、次の式が成り立つことがわかります。
h (b2) = f (b2)
したがって、次の式が成り立ちます。
f (0) × f (a2+b2) = f (a2) × f (b2)
したがって、次のことが分ります。
f (x) = c × (e k ) x2
ネイピア数 e を用いた理由は、微分しても積分しても変化しないので積分が簡単だからです。ある関数が確率密度関数であるための必要条件は −∞ 〜 +∞ の範囲で積分した値が 1 であることです。 −∞ 〜 +∞ の範囲での積分が収束するためには k は負の数でなければなりません。標準偏差を 1 とし、かつ、 −∞ 〜 +∞ の範囲での積分の値が 1 となるために k と c 値を次のようにすればいいのです。
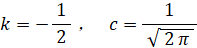
こうして、次の標準正規分布を表す確率密度関数が誕生したのです。
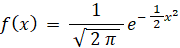
※ 参照: 大学生のための数学 > 解析学 > ガウス積分
 統計学 へ戻る
統計学 へ戻る