確率 へ戻るx
y
1−x−y
x＋y ＜ 1 つまり、 y ＜ −x＋1
x ＞ y かつ x ＞ 1−x−y のとき、つまり、 y ＜ x かつ y ＞−2 x＋1 のとき、
y＋1−x−y ＞ x つまり、 x ＜ 1/2 であれば３角形ができる。
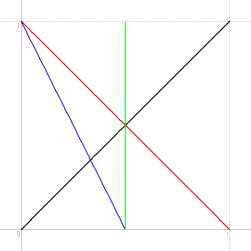
確率は 1/4 （ 面積より ）
y ＞ x かつ y ＞ 1−x−y のとき、つまり、 y ＞ x かつ y ＞−1/2 x ＋ 1/2 のとき、、
x＋1−x−y ＞ y つまり、 y ＜ 1/2 であれば３角形ができる。
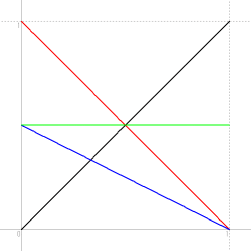
確率は 1/4 （ 面積より ）
1−x−y ＞ x かつ 1−x−y ＞ y のとき、つまり、 y ＜ −2 x＋1 かつ y ＜ −1/2 x ＋ 1/2 とき、
x ＋ y ＞ 1−x−y つまり、 y ＞−x＋1/2 であれば３角形ができる。
確率は 1/4 （ 面積より ）
したがって、答えは 25% である。