倍角の公式
　　sin 2x ＝ 2 sin x cos x　　・・・ �@
　　cos 2x ＝ 2 cos² x−1　　・・・ �A

半角の公式
　　sin² x ＝ ( 1−cos 2x ) / 2　　・・・ �B
　　cos² x ＝ ( 1＋cos 2x ) / 2　　・・・ �C


これらの公式は加法定理を用いて証明されます。

加法定理 ：
　　
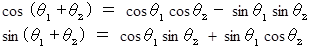
θ₁ ＝ θ₂ ＝ x として、加法定理の式に代入すると、
　　cos 2x ＝ cos² x − sin² x　＝→　2 cos² x−1　　・・・ �A
　　sin 2x ＝ 2 sin x cos x　　・・・ �@

�C は �A からすぐに導かれます。
�B を導くには次のようにします。
　　sin² x ＝ 1 − cos² x
　　　　　＝→　1 − ( 1＋cos 2x ) / 2
　　　　　＝→　( 1−cos 2x ) / 2

�@ より、次の公式が成り立つことがわかります。
　　sin x cos x ＝ 1/2 × sin 2x