ばいおりんの慣性系相対性理論

　ドの音の振動数を 1 とするとき、各音の振動数の比（R）を考えます。R を次の式で与えられるものに限って採用し音階を作ろうとしたのが、ピタゴラスです。
　　　　

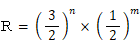
　0 以上の整数ｎと m について 1 ≦ R ≦ 2 となる R を、n を 0 から１ずつ大きくして求めていきます。
ｎ＝12 , m＝6 のとき R ≒ 2.02729 ≒ 2 として、ここで終了すると 1 ≦ R ＜ 2 の範囲で 12 個の音をゲットします。これを 1 から小さい順に並べたのが、ピタゴラス音律です。

　R ≒ 2.02729 ≒ 2 では甘すぎると考えて、ｎ＝53 , m＝30 のとき R ≒ 2.00418 ≒ 2 として、ここで終了すると 1 ≦ R ＜ 2 の範囲で 53 個の音をゲットします。この考え方は、1876年にイギリスの物理学者によって提唱されました。明治から昭和初期にかけて活躍した鉄道技術者兼物理学者兼音楽研究家の田中正平は、和音がより心地よく響くオルガン作りを目指し、この 53 音階を視野に入れていたようです。16 世紀に誕生していた「純正調」を、なぜ田中は採用しようとしなかったのか？もしかしたら「純正調」はどれみふぁそらし以外の音の振動数に対する規定があやふやだからかもしれません。

　ピタゴラス音律（12音階）の振動数比を表示するプログラム（十進BASIC ）：

　53 音階正調の振動数比を表示するプログラム（十進BASIC ）：