x y 平面上に、長方形、楕円、菱形が描かれています。
　　　　　　　
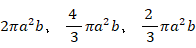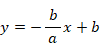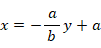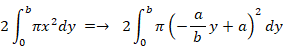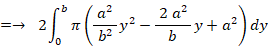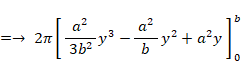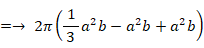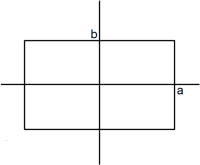
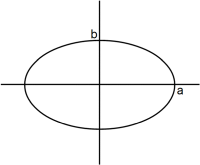
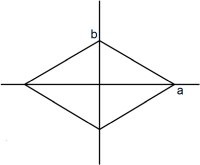
　図形の面積は、左から順に、 4ab 、 πab 、 2ab　で、その比は 4：π：2 になります。

　これらの図形の x ≧ 0 の範囲の部分を y 軸を中心に 360°回転させてできる立体の体積は、左から順に次のようになります。
　　　
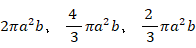
　したがって、体積の比は 3：2：1 になっていることがわかります。以上のことから、共通する軸を中心に回転させたからといって、回転体の元になる平面図形の面積比 と 回転体の体積比 とが同じになるわけではないということがわかります。