球（ 正円体 ）の中心から一瞬放たれた光は、 四方八方へと広がり、 球の内面で反射された後、 すべて同時に中心に戻ってきます。 この現象を、 球に対して等速直進運動をしている人が観察するとどうなるでしょうか？

　 等速直線運動をしている球の中心から一瞬放たれた光は、 四方八方へと広がり、 球の内面で反射された後、 すべて同時に中心に戻ってきます。 ただし、 光が放たれた瞬間の中心の位置Ａ と、 光が戻ってきた瞬間の中心の位置Ｂ とは、 異なります。 そのときの光の軌跡をすべて表しますと、 それらの集合体は、 点Ａ と 点Ｂ とを２つの中心とする 楕円体（ 楕円球 ）になります。 なぜなら、 楕円体の表面は２つの中心からの距離の和が等しい点の集合だからです。
　　　　　　　　　　　　
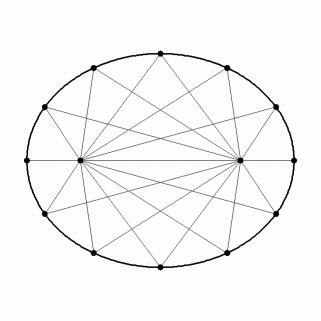
　 私は、 この楕円体のことを「 アインシュタインの楕円球 」と言っています。 次の十進BASIC のプログラムは「 アインシュタインの楕円球 」のシンプルシミュレーションです。