( 問 題 )
-
あなたは 半径
 の広い円の中心に立っています。 そして、 一様な密度と速度の雨が、 一面に斜め45度の角度で降っています。 あなたがなるべく雨に濡れないで円から脱出するには、 どの方向にどれだけの速さで等速直線移動すればいいでしょうか。 なお、 雨の地面に対する速さを
の広い円の中心に立っています。 そして、 一様な密度と速度の雨が、 一面に斜め45度の角度で降っています。 あなたがなるべく雨に濡れないで円から脱出するには、 どの方向にどれだけの速さで等速直線移動すればいいでしょうか。 なお、 雨の地面に対する速さを 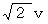 とし、 あなたの移動できる速さの最高値は、 吹いている横風の速さの10倍とします。
とし、 あなたの移動できる速さの最高値は、 吹いている横風の速さの10倍とします。-
まず、 円の半径が無限大であるとすれば、 単位時間に濡れる雨の量を比べればいいことになります。 単位時間に濡れる雨の量は、 観察を開始してから単位時間が経過するまでにあなたに接触した雨粒が、 観察の初めに存在していた空間の体積に比例します。 そこで、「 単位時間接触雨粒初期存在空間体積 」でもって、 単位時間に濡れる雨の量を表すことにします。 また、 あなたの代りに、 次のような直方体を用いて実験することにします。 横殴りの雨は、
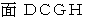 に打ちつけているものとします。
に打ちつけているものとします。

1. 風に真っ向から向かって速さ
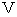 で移動する場合
で移動する場合雨に濡れる面は、
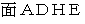 と
と 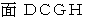 です。
です。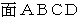 を含む面への「 単位時間接触雨粒初期存在空間体積 」の投影図を示します。 直方体は相対的に静止しています。
を含む面への「 単位時間接触雨粒初期存在空間体積 」の投影図を示します。 直方体は相対的に静止しています。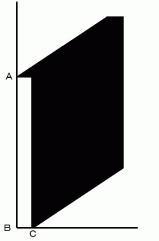
黒色に塗りつぶされた部分は、
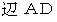 または
または 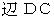 に対する「 単位時間接触雨粒初期存在空間面積 」でもあります。 これは、 次の図の黒色に塗りつぶされた部分の面積に等しいです。
に対する「 単位時間接触雨粒初期存在空間面積 」でもあります。 これは、 次の図の黒色に塗りつぶされた部分の面積に等しいです。
したがって、
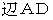 または
または 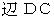 に対する「 単位時間接触雨粒初期存在空間面積 」は次のようになります。
に対する「 単位時間接触雨粒初期存在空間面積 」は次のようになります。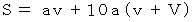
したがって、 求める「 単位時間接触雨粒初期存在空間体積 」は次のようになります。
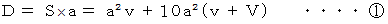
2. 風下に向かって速さ
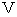 で移動する場合
で移動する場合雨に濡れる面は、
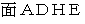 と (
と ( 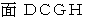 または
または 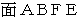 ) です。
) です。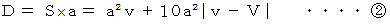
3. 風向きと垂直な方向に速さ
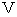 で移動する場合
で移動する場合雨に濡れる面は、
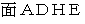 と
と 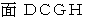 と
と 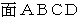 です。
です。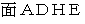 :
: 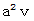
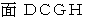 :
: 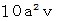
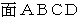 :
: 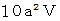
したがって、 求める「 単位時間接触雨粒初期存在空間体積 」は次のようになります。
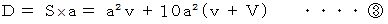
4. 風に向かって斜め45度の方向に速さ
 で移動する場合
で移動する場合雨に濡れる面は、
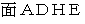 と
と 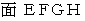 と
と 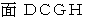 です。
です。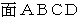 を含む面への「 単位時間接触雨粒初期存在空間体積 」の投影図を示します。 直方体は相対的に静止しています。
を含む面への「 単位時間接触雨粒初期存在空間体積 」の投影図を示します。 直方体は相対的に静止しています。
黒色に塗りつぶされた部分は、
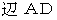 または
または 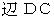 に対する「 単位時間接触雨粒初期存在空間面積 」でもあります。 これは、 次の図の黒色に塗りつぶされた部分の面積に等しいです。
に対する「 単位時間接触雨粒初期存在空間面積 」でもあります。 これは、 次の図の黒色に塗りつぶされた部分の面積に等しいです。
 を含む面への「 単位時間接触雨粒初期存在空間体積 」の投影図を示します。 直方体は相対的に静止しています。
を含む面への「 単位時間接触雨粒初期存在空間体積 」の投影図を示します。 直方体は相対的に静止しています。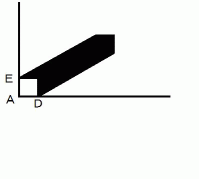
黒色に塗りつぶされた部分は、
 または
または  に対する「 単位時間接触雨粒初期存在空間面積 」でもあります。 これは、 次の図の黒色に塗りつぶされた部分の面積に等しいです。
に対する「 単位時間接触雨粒初期存在空間面積 」でもあります。 これは、 次の図の黒色に塗りつぶされた部分の面積に等しいです。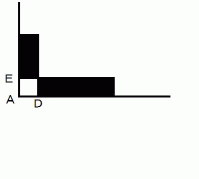
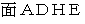 :
: 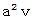
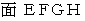 :
: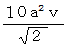
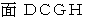 :
: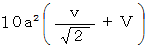
したがって、 求める「 単位時間接触雨粒初期存在空間体積 」は次のようになります。
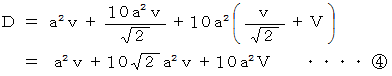
5. 風下に向かって斜め45度の方向に速さ
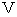 で移動する場合
で移動する場合雨に濡れる面は、
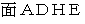 と
と 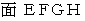 と (
と ( 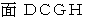 または
または 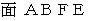 ) です。
) です。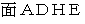 :
: 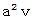
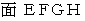 :
: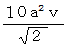
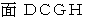 または
または 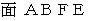 :
: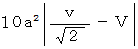
したがって、 求める「 単位時間接触雨粒初期存在空間体積 」は次のようになります。
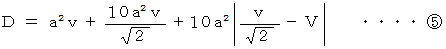
6. 以上5つのケースを考えてみました。 その結果を次に列挙します。
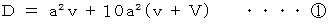
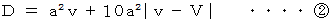
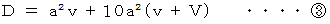
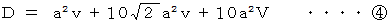
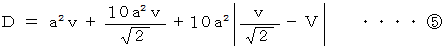
以上の式のうち、
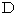 が最小になるのは、
が最小になるのは、 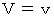 のときの
のときの  で、 そのとき
で、 そのとき 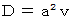 となります。
となります。そこで、 この条件を満たして円を脱出したときに、 濡れる雨の量を計算してみます。 すると、 次のようになります。
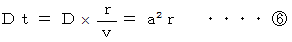
一方、 少々単位時間あたりに濡れる雨の量が多くとも、 なるべく早く円を脱出すれば、 濡れる雨の量は少なくなりますので、
 を
を 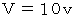 で遂行した場合に濡れる雨の量を計算してみます。 すると、 次のようになります。
で遂行した場合に濡れる雨の量を計算してみます。 すると、 次のようになります。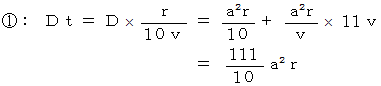
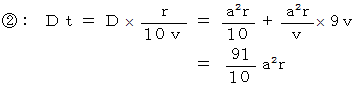
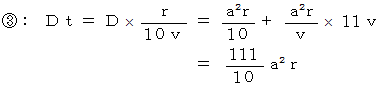
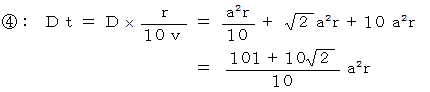
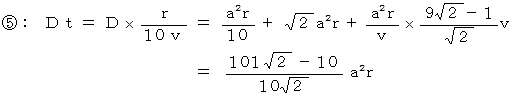
これらは、 すべて
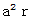 よりも大きくなっています。 したがって、
よりも大きくなっています。 したがって、  が最小であることがわかります。 つまり、 あわてないで、 風下に向かって風と同じ速度で円を脱出するのが、 頂部だけしか雨に濡れず、 濡れる雨の量を最小限にすることができることが解りました。 しかし残念ながら正解は、「 傘をさしておもむろに円を出る。」でした。 計算5963。 チャンチャン。
が最小であることがわかります。 つまり、 あわてないで、 風下に向かって風と同じ速度で円を脱出するのが、 頂部だけしか雨に濡れず、 濡れる雨の量を最小限にすることができることが解りました。 しかし残念ながら正解は、「 傘をさしておもむろに円を出る。」でした。 計算5963。 チャンチャン。 力の物理学 へ戻る
力の物理学 へ戻る