( 問 題 )
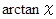 を
を  で微分すると
で微分すると 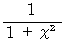 になることを示せ。
になることを示せ。( 解 答 )
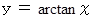 と置くと、
と置くと、 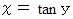 だから、
だから、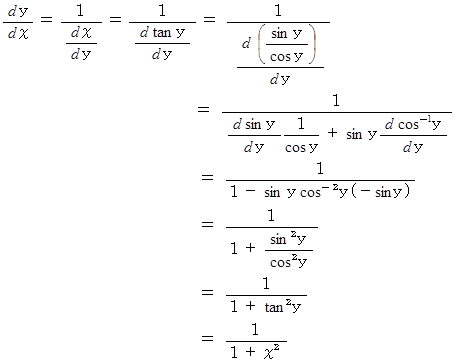
( 問 題 )
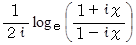 を
を  で微分すると
で微分すると 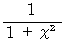 になることを示せ。
になることを示せ。( 解 答 )
ネイピア数の定義より
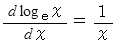 であるから、
であるから、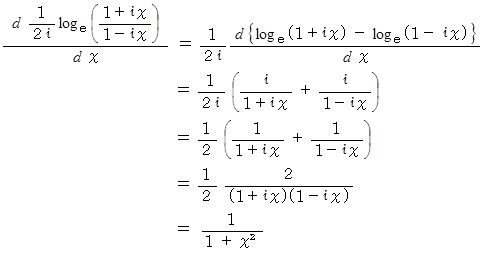
以上より、
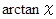 のマクローリン展開 と
のマクローリン展開 と 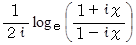 のマクローリン展開は等しいことが解ります。
のマクローリン展開は等しいことが解ります。 解析学 へ戻る
解析学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る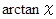 を
を  で微分すると
で微分すると 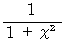 になることを示せ。
になることを示せ。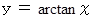 と置くと、
と置くと、 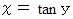 だから、
だから、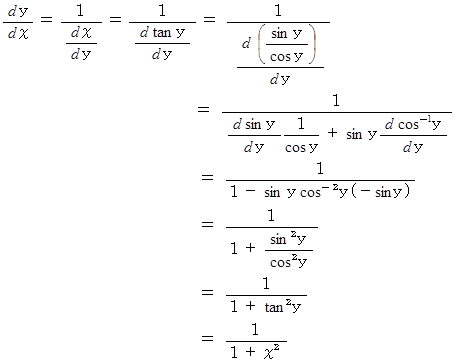
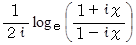 を
を  で微分すると
で微分すると 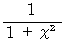 になることを示せ。
になることを示せ。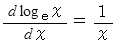 であるから、
であるから、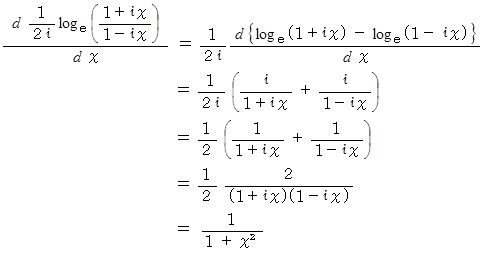
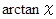 のマクローリン展開 と
のマクローリン展開 と 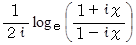 のマクローリン展開は等しいことが解ります。
のマクローリン展開は等しいことが解ります。