単位は記載していませんが、 SI単位系であるとします。 重力加速度を
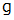 とします。
とします。質量
 の重りが付いた 自然長
の重りが付いた 自然長  バネ定数
バネ定数 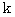 のバネを天井から吊らします。
のバネを天井から吊らします。( 問 1 )
このときバネの長さはいくらになっているでしょうか?
( 解 答 )
-
このときバネが
 伸びているとすると、 力のつり合いから次の式が成り立ちます。
伸びているとすると、 力のつり合いから次の式が成り立ちます。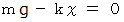
したがって
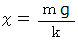 したがって答えは
したがって答えは 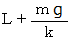 です。
です。この重りを手で持ってバネの長さが
 になるまで持ち上げます。 このときに手のする仕事を求めなさい。
になるまで持ち上げます。 このときに手のする仕事を求めなさい。( 解 答 )
-
重りを
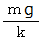 の高さ持ち上げるときの仕事を求めればいいのですが、 手が重りに加えなければならない力 (
の高さ持ち上げるときの仕事を求めればいいのですが、 手が重りに加えなければならない力 ( 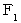 ) は次第に大きくなります。 それは次の式で表されます。
) は次第に大きくなります。 それは次の式で表されます。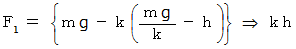
したがって、 仕事は次のようになります。
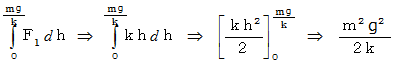
この重りを手で持ってバネの長さが
 になるまで持ち上げます。 このときにバネのする仕事を求めなさい。
になるまで持ち上げます。 このときにバネのする仕事を求めなさい。( 解 答 )
-
バネが重りに及ぼす力 (
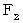 )
)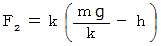
バネが重りに対してする仕事
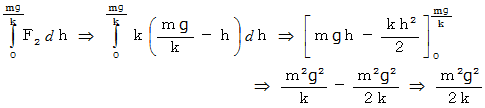
この重りを手で持ってバネの長さが
 になるまで持ち上げます。 このときに、 手 と バネ が協力してする仕事と重りに加わるエネルギーを求めなさい。
になるまで持ち上げます。 このときに、 手 と バネ が協力してする仕事と重りに加わるエネルギーを求めなさい。( 解 答 )
-
手が重りに対してする仕事 と バネが重りに対してする仕事 の和
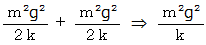
手が重りに及ぼす力 と バネが重りに及ぼす力 の和
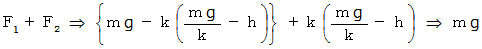
重りの得る一様な重力場における位置エネルギー
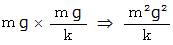
この重りを手で持ってバネの長さが
 になるまで持ち上げたあと、 手を離すと重りは振動をしますが、 このときバネは最高でいくらの長さになるでしょうか?
になるまで持ち上げたあと、 手を離すと重りは振動をしますが、 このときバネは最高でいくらの長さになるでしょうか?( 解 答 )
-
バネが
 伸びているときの重りの速さを
伸びているときの重りの速さを  とします。バネの自然長の位置の高さを
とします。バネの自然長の位置の高さを  として、 エネルギー保存の法則のを作ると次のようになります。
として、 エネルギー保存の法則のを作ると次のようになります。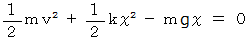
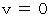 のとき、 バネは最短または最長になります。
のとき、 バネは最短または最長になります。そこで、 エネルギー保存の法則の式に
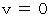 を代入すると、
を代入すると、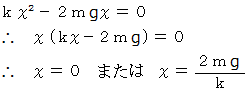
したがって、 答えは
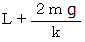 です。
です。この重りを手で持ってバネの長さが
 になるまで持ち上げたあと、 手を離すと重りは振動をしますが、 このとき重りの速さは最高でいくらになるでしょうか?
になるまで持ち上げたあと、 手を離すと重りは振動をしますが、 このとき重りの速さは最高でいくらになるでしょうか?( 解 答 )
-
バネが
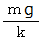 伸びているときの重りの速さが最速です。 このときの速さはエネルギー保存の法則の式から次のようになります。
伸びているときの重りの速さが最速です。 このときの速さはエネルギー保存の法則の式から次のようになります。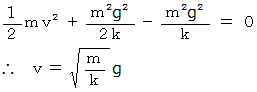
 力学 へ戻る
力学 へ戻る