質量 m 1 (kg) の物質A と 質量 m 2 (kg) の物質B からなる2物質系について考えます。
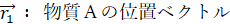
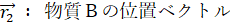
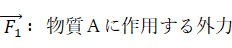
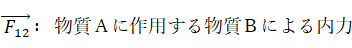

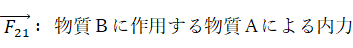
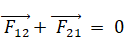
系全体の運動量は次のように表されます。

この式を t で微分します。
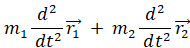
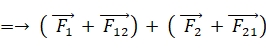
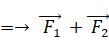
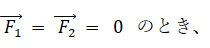
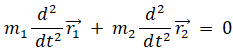
したがって、外力が作用していない場合は、次の運動量保存則が成り立っていることが分かります。
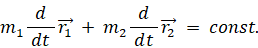
例えば、衝突の前後で2つの物質の運動量の合計が変化しないことがあります。
【 例 題 】
-
簡略化のため SI単位の記載を略します。
床と物質Aとの間の動摩擦係数は0です。
物質Aと物質Bとの間の動摩擦係数は μ です。
物質Aの質量は M で、物質Bの質量は m です。

今、物質Bを矢印の方向に初速 v0 で物質A上を滑るように打ち出しました。
(1) 物質Bが物質Aに対して静止した直後から以降の物質Aの床に対する速さを求めよ。
(2) 物質Bが物質Aに対して静止するまでにかかった時間を求めよ。
-
(1)
-
物質Bが物質Aに対して静止した直後から以降は、物質Bも物質Aも床に対して同じ速度で等速直線運動をします。その速さを v0 とします。2つの物質には遠隔力以外には内力しか作用しないので、運動量保存法則が成り立ちます。よって、
m v0 = ( m+M ) v
よって、
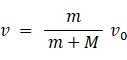
-
物質Bが物質Aに対して静止するまでにかかった時間を t とします。
物質Aは物質Bの物質Aに対する動摩擦力の反作用( 大きさ μmg )によって等加速度直線運動( 加速度の大きさを a とします )をします。物質Aの床に対する初速は0です。したがって、次の式が成り立ちます。
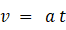
よって、
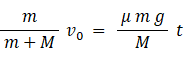
よって、
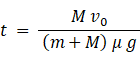
 力学 へ戻る
力学 へ戻る