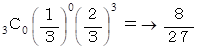
サイコロを振って選ばれた3つの数の中に 1 個だけ3の倍数が含まれている確率 :

サイコロを振って選ばれた3つの数の中に2個だけ3の倍数が含まれている確率 :
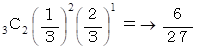
サイコロを振って選ばれた3つの数がすべて3の倍数である確率 :
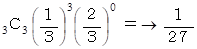
サイコロを振って選ばれた3つの数の中に 1 個も3の倍数が含まれていなくて、 かつ、 その中から無作為に 1 個の自然数を抽出したときそれが3の倍数である確率 :
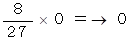
サイコロを振って選ばれた3つの数の中に 1 個だけ3の倍数が含まれていて、 かつ、 その中から無作為に 1 個の自然数を抽出したときそれが3の倍数である確率 :
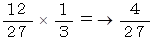
サイコロを振って選ばれた3つの数の中に2個だけ3の倍数が含まれていて、 かつ、 その中から無作為に 1 個の自然数を抽出したときそれが3の倍数である確率 :
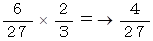
サイコロを振って選ばれた3つの数がすべて3の倍数であって、 かつ、 その中から無作為に 1 個の自然数を抽出したときそれが3の倍数である確率 :
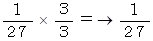
したがって、 求める答えは、
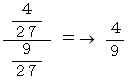
 確率 へ戻る
確率 へ戻る