全体集合としてのある物質集団がある。
その物質集団が、第一集合に含まれる確率は P である。
第一集合に含まれているその物質集団の中から無作為に抽出した個体が第二集合にも含まれる確率は A1 である。
第一集合に含まれていないその物質集団の中から無作為に抽出した個体が第二集合に含まれる確率は A2 である。
さて、この物質集団の中から無作為に1個を抽出して調査たところ、その個体は第ニ集合に含まれていた。
この個体が第一集合にも含まれている確率を求めよ。
| 第二集合に含まれる | 第二集合に含まれない | |
| 第一集合に含まれる | P A1 | P ( 1-A1 ) |
| 第一集合に含まれない | ( 1-P ) A2 | ( 1-P ) ( 1-A2 ) |
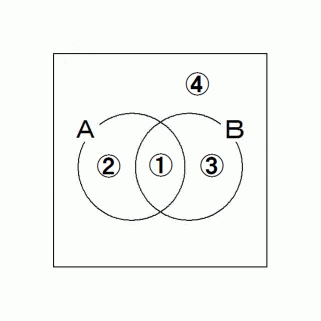
確率分布: ① + ② + ③ + ④ = 1
A: 先発命題( 真偽不明;確率的予想可 )
B: 後発命題 = 真であるという事実 = 入手情報
A
調査物質が集合Bに含まれているという情報を得た時点で、
それが集合Aにも含まれている確率が、条件付き確率 である。
条件付き確率 = ① ÷ ( ① + ③ )
集合A: 2つとも金貨が入っている箱
集合B: 箱から取り出された貨幣であり、かつ、金貨である貨幣
■ 後発命題が真である確率:
選択した箱の中のから取り出した1個の貨幣が金貨である確率
1/3 × 1 + 1/3 × 0 + 1/3 × 1/2 =→ 3/6 =→ 1/2
□ 後発命題が真であり、かつ、先発命題が真である確率:
2つとも金貨が入っている箱を選び かつ その中から1個貨幣を取り出すと金貨である 確率
1/3 × 1 =→ 1/3
求める条件付き確率:
選択した箱の中のから取り出した1個の貨幣が金貨であった。
その箱が2個とも金貨の入っている箱である確率は、
□ ÷ ■ = 1/3 ÷ 1/2 =→ 2/3
 確率 へ戻る
確率 へ戻る