※ この検査は、
感度( 偽陰性の少なさを表す度合い ): 95%
特異度( 偽陽性の少なさを表す度合い ): 90%
この5年間の統計より、疾患Aの罹患率は 0.1% であることが分かっている。
したがって、この時点で無作為に選ばれたある人が疾患Aに罹患している確率( 原因確率 )は 0.1% である。
また、無作為に選ばれたある人が検査を受けて陽性になる確率( 結果確率 )は 10.085% である。
なぜなら、 0.1% × 95% + 99.9% × 10% =→ 1008.5 %2 =→ 10.085%
また、因果確率は、感度と同じ 95% である。
無作為に選ばれたある人が検査を受けたところ、陽性であった。( そういった情報を知った )
そのために、その人が疾患Aに罹患している確率は 0.1% から 0.942% へと変化した。
( 考えようによっては大した変動ではない。)
その理由を考えてみよう。
-
因果確率 : 疾患Aに罹患しているが検査結果が陽性になる確率は 95% である。
情報後原因確率( 条件付き確率 ): 検査結果が陽性の人が疾患Aに罹患している確率は P% である。
ベイズの定理:
情報後原因確率 = 因果確率 ×( 原因確率 ÷ 結果確率 )
= ( 原因確率 × 因果確率 ) ÷ 結果確率 = 条件付き確率
P% = 95% ×( 0.1% ÷ 10.085% ) ≒→ 0.942 %
以上のことを 条件付き確率 の考え方で解くと次のようになります。
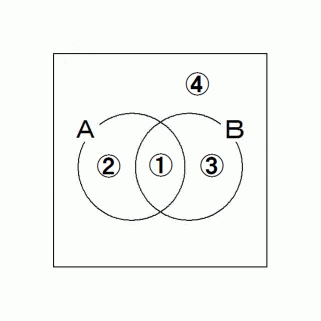
確率分布: ① + ② + ③ + ④ = 1
A: 先発命題( 真偽不明;確率的予想可 )
B: 後発命題 = 真であるという事実 = 入手情報
A
調査物質が集合Bに含まれているという情報を得た時点で、
それが集合Aにも含まれている確率が、条件付き確率 である。
条件付き確率 = ① ÷ ( ① + ③ )
-
① 無作為に選ばれたある人が疾患Aに罹患している上に、検査が陽性となる確率
0.1% × 95% =→ 9.5 %2 =→ 0.095 %
③ 無作為に選ばれたある人が疾患Aに罹患していない上に、検査が陽性となる確率
99.9% × 10% =→ 999 %2 =→ 9.99 %
よって、無作為に選ばれたある人が検査が陽性であったことを知ったという条件下で、無作為に選ばれたある人が疾患Aに罹患している確率は ① ÷ (①+③) =→ 0.00942 =→ 0.942 % である。
 確率 へ戻る
確率 へ戻る