ある植物は赤または青の花をつけ、 また花弁数は偶数である場合と奇数である場合があります。 その植物が群生している所で調査したところ、 次のような結果でした。
- 花弁の数が偶数であるものと奇数であるものとの比は 2:3 である。
- 青色の花の数と赤色の花の数の比は 3:2 である。
- 青色の花については、 花びらの数が偶数のものと奇数のものが半々である。
花びらの数が偶数であるものから任意に1つを選んだとき、 その花が青色である確率はいくらでしょうか?
ベイズの定理の式を具体化しやすくするには、 包含関係を表すベン図を用いる方法と、 相関関係表を用いる場合とがありますが、 今回は後者を用いることにしましょう。
| 花 の 色 | ||||
| 青 | 赤 | 計 | 花弁数 | 偶数 | 15 | 20 | 奇数 | 15 | 30 |
| 計 | 30 | 20 | 50 | |
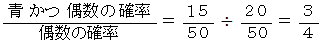
ベイズの定理を理解するために、 次のような十進BASIC のプログラムを作ってみました。
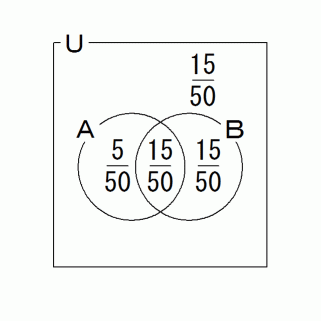
集合A : 花弁の数が偶数であるもの
集合B : 花の色が青いもの
 十進
十進