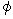
ベクトル :
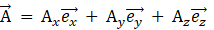
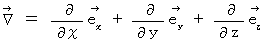 ( ハミルトン演算子 )
( ハミルトン演算子 )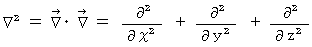 ( ラプラス演算子
( ラプラス演算子  )
)勾配 :
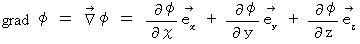
 は、 スカラー を ベクトル に変換する演算子である。
は、 スカラー を ベクトル に変換する演算子である。勾配とは、 ある点における、 微小変位によってスカラー場が最も大きく変化する方向
を向き、 その微小変位あたりの微小変化量と同じ大きさを持つベクトルである。
発散 :
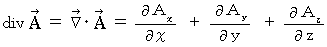
 は、 ベクトル を スカラー に変換する演算子である。
は、 ベクトル を スカラー に変換する演算子である。発散とは、 ある点における、 単位体積あたりのベクトル場の湧き出し量を表すスカラ
ーである。
回転 :
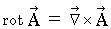
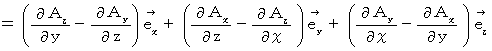
 は、 ベクトル を ベクトル に変換する演算子である。
は、 ベクトル を ベクトル に変換する演算子である。回転とは、ある点における、単位面積あたりの渦の強さを表すベクトルである。
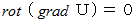
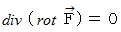
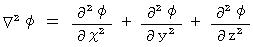
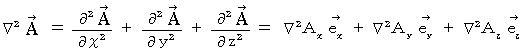
ベクトル場 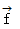 が
が 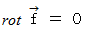 を満たすとき、
を満たすとき、 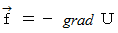 を満たすスカラー場
を満たすスカラー場 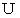 が存在する。 スカラー場
が存在する。 スカラー場 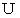 はベクトル場
はベクトル場 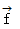 のポテンシャル ( スカラーポテンシャル ) と言われる。
のポテンシャル ( スカラーポテンシャル ) と言われる。
ベクトル場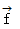 が
が  を満たすとき、
を満たすとき、 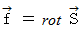 を満たすベクトル場
を満たすベクトル場 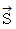 が存在する。 ベクトル場
が存在する。 ベクトル場 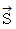 はベクトル場
はベクトル場 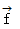 のベクトルポテンシャルと言われる。
のベクトルポテンシャルと言われる。
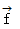 が
が 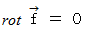 を満たすとき、
を満たすとき、 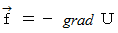 を満たすスカラー場
を満たすスカラー場 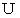 が存在する。 スカラー場
が存在する。 スカラー場 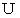 はベクトル場
はベクトル場 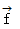 のポテンシャル ( スカラーポテンシャル ) と言われる。
のポテンシャル ( スカラーポテンシャル ) と言われる。ベクトル場
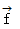 が
が  を満たすとき、
を満たすとき、 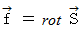 を満たすベクトル場
を満たすベクトル場 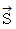 が存在する。 ベクトル場
が存在する。 ベクトル場 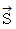 はベクトル場
はベクトル場 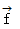 のベクトルポテンシャルと言われる。
のベクトルポテンシャルと言われる。勾配の例 その1 :
スカラー場 :
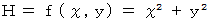
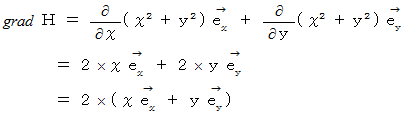
このスカラー場の勾配は、 位置ベクトルの2倍に等しい。
勾配の例 その2 :
スカラー場 :
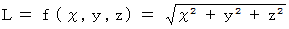
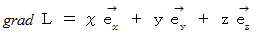
このスカラー場の勾配は、 位置ベクトルに等しい。
勾配の例 その3 :
スカラー場 :
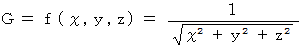
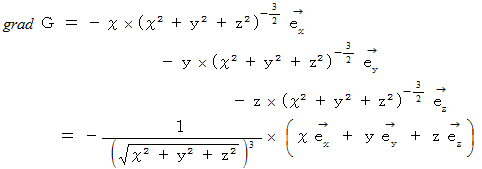
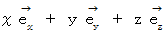 の大きさは
の大きさは 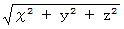 だから、
だから、 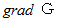 の大きさは
の大きさは 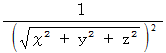 である。 したがって、 このスカラー場の勾配は、 位置ベクトルの大きさの2乗の逆数に等しくて、 位置ベクトルとは逆向きであることがわかる。
である。 したがって、 このスカラー場の勾配は、 位置ベクトルの大きさの2乗の逆数に等しくて、 位置ベクトルとは逆向きであることがわかる。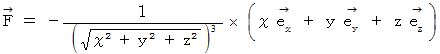 と置くと、
と置くと、 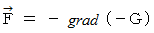 となるので、 スカラー場
となるので、 スカラー場  は ベクトル場
は ベクトル場 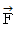 のスカラーポテンシャルである。 スカラー場
のスカラーポテンシャルである。 スカラー場  は
は 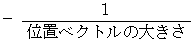 つまり
つまり 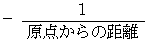 であり、 ベクトル場
であり、 ベクトル場 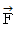 は、 大きさが原点からの距離の2乗の逆数に等しくて、 原点を向いている。 このようなベクトル場の例は、 原点に存在する質量
は、 大きさが原点からの距離の2乗の逆数に等しくて、 原点を向いている。 このようなベクトル場の例は、 原点に存在する質量  の物質が産生する重力場である。
の物質が産生する重力場である。物理学には、 「 位置エネルギー 」 という物理量があり、 普通は一様な重力場という条件の下での相対的な量であるが、 スカラーポテンシャル ( ポテンシャル ) は、 「 絶対的位置エネルギー 」 の指標となっている。 つまり、 そこに質量
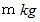 の物質が存在するとき、 重力場を産生している物質に対するその物質の絶対的位置エネルギーは、 スカラーポテンシャルに
の物質が存在するとき、 重力場を産生している物質に対するその物質の絶対的位置エネルギーは、 スカラーポテンシャルに  をかけた値になっている。
をかけた値になっている。 ベクトル解析 へ戻る
ベクトル解析 へ戻る