一階常微分方程式（ 正規形 ）は、 次のような形をしています。
　　　　


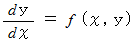
（ 例 題 ）
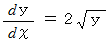　　　　　を解け。

（ 解 答 ）

微分方程式を解くとは、y が x を用いたどんな関数で表すかを明らかにすることです。
　
　　　　
　　　　

　
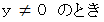
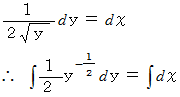
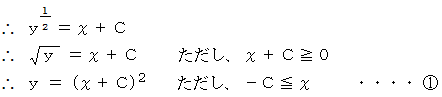
　　　常微分方程式が成り立ちます。 したがって、 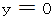も解の１つです。

　 は一般解です。これをグラフに書いてみることにしましょう。 まず、 たとえば 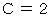のときを描くと、 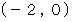を頂点とする下に凸でＸ軸に接する放物線の 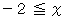の部分になります。 はいろんな値をとっていいわけですから、 無数の半放物線を書くことができます。 これらの放物線に共通するのは、 y の座標値が同じならば傾きが同じであることと、 下に凸であることと、 Ｘ軸に接することです。

　 さて、 曲線群と常に接線を共有する曲線のことを、 包絡線といいます。 したがって、 この場合は、 Ｘ軸が一般解の曲線群の包絡線であるということです。 Ｘ軸は 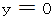のグラフに一致します。 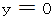もこの一階常微分方程式の解です。 一階常微分方程式は、 グラフでは、 座標点ごとの傾きを表す式であり、 この例題のように、 その傾きを接線とする一連の曲線群で表されます。 この曲線群に対する包絡線が存在するとき、 それを表す式は同じ一階常微分方程式の解となっており、 それは一般解と区別され、 特解と言われます。