１クラス36名、 １学年10クラス の高等学校の全クラスで、 同じ日に生まれた人があるクラスがいくつあるのか調査したところ、 25クラスもあったとのことです。 なんかの間違いではないでしょうか？

　 そこで、 次のように考えました。
　 あるクラスにおいて、 生まれた月ごとに生徒が集まると、 各月が３名ずつになりそうです。 そこで、 誕生日が同じである確率は次のようにして概算できそうです。
　　　　　
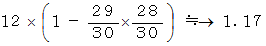
えっ！？　確率が を超えている！
というわけで、 もうすこしマシな確率の概算は次のようなものです。
　　　　　

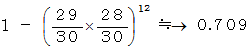
正確な確率は、 次の十進BASIC のプログラムで見てください。

シミュレーション：

集まった人数 人　　　



23人以上のクラスでは、 誕生日が同じ人がいる確率が 50% 以上になります。





　 今度は、 １人づつ集めていって初めて誕生日が同じ人が出現するまでに平均何人を集めなければならないのかをシミュレートします。

　

　 今度は、 自分と誕生日が同じ人がいる確率が50%を超えるまでに平均何人を集めなければならないのかを考えます。
求める人数をｎ人とすると、自分と誕生日が同じ人がいる確率は次のようになります。
　　　
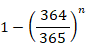
これが50%を超えるには、ｎは 253以上 になります。


　再び元の問題に帰ります。誕生日が同じ人がいる確率が 50% 以上になるには何人以上のクラスである必要があるのか？ また、誕生日が同じ人がいる確率が 95% 以上になるには何人以上のクラスである必要があるのか？ を考えます。

　ｎ人クラスの場合、誕生日が同じ人がいる確率は次の式で表されます。
　　　
　　　　　　　　　　　　　

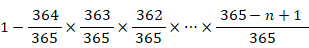
　これが 0.5 になるような ｎの値を求めたいのですが、プログラミングしなければなりません。そこで、上式の近似式を作ります。
　　　
　　　　　　　　
　　　　　　　　
　　　　　　　　

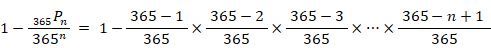
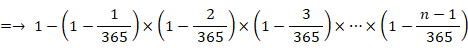
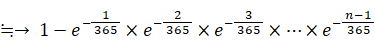
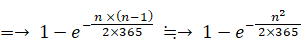
　　　※ 指数関数のマクローリン展開
　　　　　　
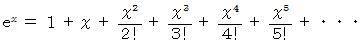
　　　　　　　　　 x が０に近いとき、 e^x ≒ １＋ x

　この近似式を用いて、誕生日が同じ人がいる確率が 0.5 になるような ｎの値を求めてみましょう。
　　　
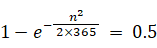
　　　よって、
　　　　　
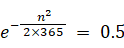
　　　よって、
　　　　　
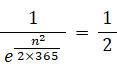
　　　よって、
　　　　　
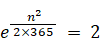
　　　よって、
　　　　　
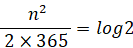
　　　よって、
　　　　　
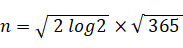
　　　よって、
　　　　　
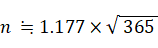
　　　よって、
　　　　　

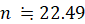
　次に、誕生日が同じ人がいる確率が 0.95 になるような ｎの値を求めてみましょう。
　　　
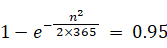
　　　よって、
　　　　　
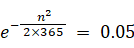
　　　よって、
　　　　　
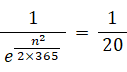
　　　よって、
　　　　　
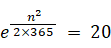
　　　よって、
　　　　　
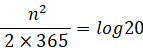
　　　よって、
　　　　　
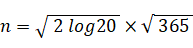
　　　よって、
　　　　　
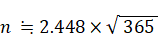
　　　よって、
　　　　　

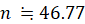
　誕生日が同じ人がいる確率を十進BASICで以下のようなプログラムを作って計算してみると、47人クラスで0.9548%、46人クラスで0.9483% になりますので、近似式を用いて導き出した結果が正しいことが確認できます。

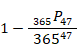　　　 を求めるプログラムの内容 ：