微分の概念には、「 極限値ゼロ 」の考え方が入っています。 微分は次のように定義されます。
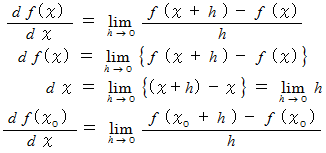
物理学の微分の例は、 変位と経過から求められる速度です。 速度は時刻に対して与えられる値です。 ( ただし、 平均速度は時間に対して与えられる値です。)
直線上を一方方向に移動している点
 について考えます。 点
について考えます。 点 の時刻
の時刻 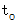 における位置を
における位置を 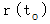 、 時刻
、 時刻 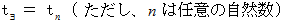 における位置を
における位置を 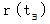 とします。 点
とします。 点 の 時刻
の 時刻 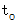 から 時刻
から 時刻 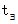 における変位は
における変位は  であり、 その間の平均速度の大きさは次の式で表されます。
であり、 その間の平均速度の大きさは次の式で表されます。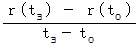
この式は、 変位( 移動空間 )を経過( 移動時間 )で割ったもので、 横軸を経過、 縦軸を変位とする直交2次元グラフでは、 傾きを表すものになっています。
 コメント : 変位
コメント : 変位  の物質でも、 移動時間は
の物質でも、 移動時間は  ではありません。
ではありません。時刻
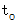 から 時刻
から 時刻 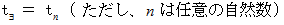 までの時間を
までの時間を  当分したときの、 最初の時間帯の点
当分したときの、 最初の時間帯の点 の平均速度の大きさは、 次の式で表されます。
の平均速度の大きさは、 次の式で表されます。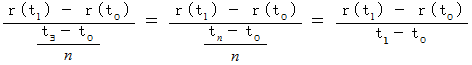
この式で
 が無限大の場合は、 この場合も
が無限大の場合は、 この場合も 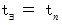 で、 時刻
で、 時刻 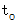 における点
における点 の速度の大きさになります。 したがって、 時刻
の速度の大きさになります。 したがって、 時刻 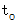 における点
における点 の速度の大きさは次のように表わされます。
の速度の大きさは次のように表わされます。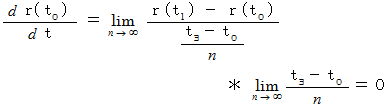
以上の物理学の微分の例を一般化して、 次のように表すことにします。 これは、 微分の概念を表す式です。
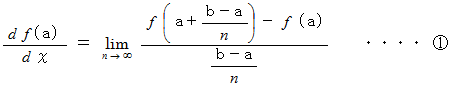
さらに、 この式は次のように一般化することができます。
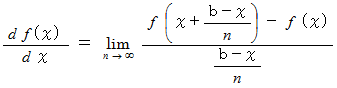
さらに、
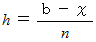 と置くと、 上の式は、 次のように一般的な微分の概念を表す式になります。
と置くと、 上の式は、 次のように一般的な微分の概念を表す式になります。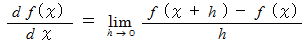
積分の概念には、 デジタル化の考え方と「 極限値ゼロ 」の考え方が入っています。 それはつまり、 人工的なデジタルに「 極限値ゼロ 」の考え方を加えると、 自然的なアナログを作ることができるということです。 積分は次のように定義されます。
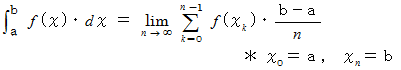
xk = a + ( b−a )× k / n
 コメント :
コメント :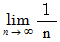 は、 数列
は、 数列 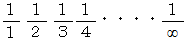 が
が  に収束す
に収束するということを表す記号であり、 これは、 無限大の考え方ではなく、
「 極限値ゼロ 」の考え方です。
※ 参照: 大学生のための数学 > 解析学 > スカラー場の線積分のイメージ
この式は、 次のようにも表すことができます。
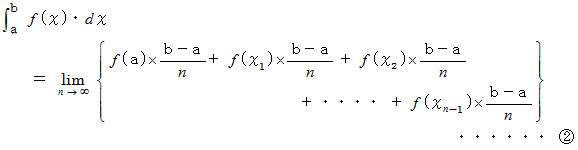
 の微分の式と
の微分の式と  の積分の式を比べてください。
の積分の式を比べてください。  は
は 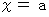 の点に対して与えられる値であるのに対して、
の点に対して与えられる値であるのに対して、  は
は 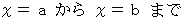 の線に対して与えられる値です。
の線に対して与えられる値です。物理学の積分の例は、 速度と経過から求められる変位です。 変位は時間に対して与えられる空間の値です。
直線上を一方方向に移動している点
 について考えます。 点
について考えます。 点 の時刻
の時刻 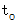 における速度の大きさを
における速度の大きさを 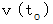 、 時刻
、 時刻 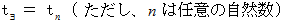 における速度の大きさを
における速度の大きさを 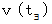 とします。
とします。 です。 微小変位の総和をとれば、 全体の変位になりますので、 全体の変位は次の式で与えられます。
です。 微小変位の総和をとれば、 全体の変位になりますので、 全体の変位は次の式で与えられます。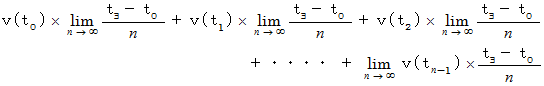
この式は、 次の式と同じものです。
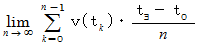
この式は、 次の式と同じものです。
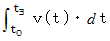
「 微小変位の総和をとれば、 全体の変位になる。」は、 次のようにも表現することができます。「 速度に微小経過をかけたものの総和をとれば、 全体の変位になる。」 これは積分の考え方です。「 速度を経過で積分すれば変位になる。」です。 積分とは、
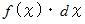 の デジタル的な総和
の デジタル的な総和 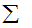 でなく、 アナログ的な総和
でなく、 アナログ的な総和 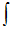 なのです。
なのです。 解析学 へ戻る
解析学 へ戻る