質量 3m kg、長さ Lm の内部が均一な棒Aがあります。 棒Aの線密度は 3m /L kg/m です。
質量 m kg、長さ 2L/ 3 m の内部が均一な棒Bがあります。 棒Bの線密度は 3m / 2L kg/m です。
質量 2m kg、長さ L/ 3 m の内部が均一な棒Cがあります。 棒Cの線密度は 6m /L kg/m です。
棒A と 棒B と 棒C は同じ太さです。 棒B と 棒C を接合して 質量 3m kg 長さ Lm の棒Dにします。 棒Dの重心はちょうど接合部になります。

※ 上が棒Aで、下が棒Dです。
棒Aが一端を中心に回転するときの慣性モーメント(IA )は、次の式で表されます。
IA = m L2
※ 参照: 剛体の力学 > 棒の慣性モーメント
棒DのC側の一端を中心に回転するときの慣性モーメント(ID )は、次の式で表されます。
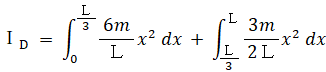
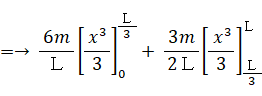


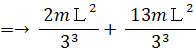
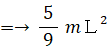
棒Aの一端を空中で支点として固定し、支点を含む鉛直面上で自由に回転できるようにします。棒Aを手で持って垂直に立ててからそっと手を離すと棒Aは転倒を開始します。棒Aの他端が最下点に達したときの角速度( ωA rad/s )を求めてみましょう。 重力加速度を g とします。
力学的エネルギー保存則より次の式が成り立ちます。
3/2 mgL = −3/2 mgL + 1/2 × 3m × ( L/ 2 × ωA ) 2 + 1/2 × IA × ωA 2
※ 1/2 × 3m × ( L/ 2 × ωA ) 2 は重心の運動エネルギーです。
これを解くと、答えは次のようになります。

棒DのC側の端を空中で支点として固定し、支点を含む鉛直面上で自由に回転できるようにします。棒Dを手で持って垂直に立ててからそっと手を離すと棒Dは転倒を開始します。棒Dの他端が最下点に達したときの角速度( ωB rad/s )を求めてみましょう。
力学的エネルギー保存則より次の式が成り立ちます。
3/3 mgL = −3/3 mgL + 1/2 × 3m × ( L/ 3 × ωB ) 2 + 1/2 × IB × ωB 2
これを解くと、答えは次のようになります。
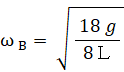
最後に間違った考え方を紹介しましょう。もし、棒Dの重心を2つの重心の合成と考えて式を立てると次のようになります。
2/3 mgL + 2/6 mgL
= −2/3 mgL − 2/6 mgL + 1/2 × m × ( 2L/ 3 × ωB ) 2 + 1/2 × 2m × ( L/ 6 × ωB ) 2 + 1/2 × IB × ωB 2
これを解くと次のようになり、この重心分解の考え方が誤りであることが分かります。

 剛体力学 へ戻る
剛体力学 へ戻る