（１） 複素数の大きさ

　　　　　
　 上記のような２つの複素数があるときに、 と は互いに複素共役な数であると言います。 互いに複素共役な数は同じ大きさであり、 その複素数たちの大きさは次のように表されます。
　　　　　

（２） 複素数の内積

次のような、無限次元ベクトルが２つあるとします。
　　　　　
　 ベクトルの成分が複素数の場合、 に を内積させる演算は、 一般的には次のように表されます。
　　　　　
　 ディラックは、 ベクトルの成分が複素数の場合、 に を内積させる演算を次のように表しました。 いわゆる「 ブラ・ケット 」です。
　　　　　
　 私は、 ベクトルの成分が複素数の場合、 に を内積させる演算を次のように表すことにしています。
　　　　　

　 複素数の場合は、 実数の場合とは異なり、 に を内積させる演算の結果と に を内積させる演算の結果 とは異なります。 それらは、 お互いに複素共役な数になります。 それは、 次の式を見ると解ります。
　　　　　

（３） 確率論解釈

　 実数の場合、 と の内積は の大きさの２乗になっていますが、 複素数においても、 と の内積は の大きさの２乗になっています。
　　　　　
　 も も大きさが であるとします。 このとき、 量子力学では、 や を波のような全体の状態であるとし、 それらは「 規格化 」されていると言います。 規格化されているとき、 全体と部分の内積は、 その部分が全体の構成にとってどれくらいの比率で貢献しているのかを表します。
　　　　　
　 量子力学の確率論解釈では、「 観察とは、 無理やりにどれかの部分に全体を内積させた結果を得ることである。」とします。

（４） エルミート演算子

　 ベクトルの成分が複素数になっているあるベクトルを他のベクトルに変換する演算子を、 演算テンソル で表します。 の表現行列の要素は複素数です。 このとき、 次のような式が成り立っていたとします。
　　　　　
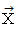　 この式の意味は、「 に『 に を作用させて得られたベクトル 』を内積させたものは、『 に の表現行列の随伴行列を表現行列とする演算テンソルを作用させて得られたベクトル 』に 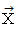を内積させたものに等しい。」ということです。 このとき、 を「 エルミート共役な演算子 」と言います。 また、 随伴行列（ 転置して複素共役を取った行列 ）が自分自身に等しい行列は、 エルミート行列 と言われます。「 エルミート共役な演算子 」の表現行列がエルミート行列であるとき、 その演算子は「 エルミート演算子 」と言われます。 量子力学では、「 すべての物理量はエルミート演算子である。」として、「 その物理量を観察することは、 全体の状態を表す無限次元の波動関数ベクトルに、 そのエルミート演算子を作用させることである。」とします。

（５） 追伸： 実数世界との対応

　 ベクトルの成分が実数になっているあるベクトルを他のベクトルに変換する演算子を、 演算テンソル で表します。 の表現行列の要素は実数です。 任意のベクトル と について、 次の式が成り立ちます。
　　　　　
　 転置行列が自分自身に等しい行列は、 対称行列 と言われます。 の表現行列が対称行列のとき、 は「 対称演算子 」になります。 対称演算子は、「 ユークリッド空間での線形変換 」（ 対称変換 ）を担う演算テンソルです。