（ 問題１）

　 上下２つの引き出しの付いた箱が３つあり、 外見では区別ができません。 Ａ の箱に
は上下の引き出しに赤玉が１個ずつ入っており、 Ｂ の箱には上下の引き出しに白玉が１個ずつ入っており、 Ｃ の箱には上の引き出しに赤玉が１個、 下の引き出しに白玉が１個入っています。 この３つの箱の中から１つを無作為に選んで、 上の引き出しを開けたところ赤玉が入っていました。 この箱の下の引き出しに赤玉が入っている確率はいくらでしょうか？

　　　　　

（ 解答 ）

　 Ｂ の箱は最初から存在していないと考えます。 この時点で、 選んだ箱がＡ である確率は ２分の１ であり、 選んだ箱がＣ である確率は ２分の１ です。 したがって、 この箱の下の引き出しに赤玉が入っている確率は、 次のようにして ２分の１ であることが解ります。
　　　　　


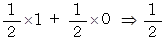
この問題の一部を次のように書き換えます。

　 Ｃ の箱には、 一方の引き出しに赤玉が１個、 他方の引き出しに白玉が１個入っています。
　　　　　　　( 上の引き出しに赤玉が入っている確率は 1/2 です。）
すると、 この問題は 「 ベルトランの箱 」 になり、 答えは 2/3 になります。 次の問題を見てください。

（ 問題 ２ ）

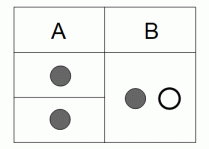
　 上下２つの引き出しの付いた箱が２つあり、 外見では区別ができません。 Ａ の箱には上下の引き出しに赤玉が１個ずつ入っており、 Ｂ の箱には、 一方の引き出しに赤玉が１個、 他方の引き出しに白玉が１個入っています。 ( 上の引き出しに赤玉が入っている確率は 1/2 です。） この２つの箱の中から１つを無作為に選んで上の引き出しを開けたところ、赤玉が入っていました。 この箱の下の引き出しに赤玉が入っている確率はいくらでしょうか？

　　　　　　　　

（ 解答 ）

　 この問題は、 「 この箱の下の引き出しに赤玉が入っている確率はいくらでしょうか？」 という部分を 「 箱Ａ を選んでいた確率はいくらでしょうか？」 とか 「 この赤玉が箱Ａ の中の赤玉である確率はいくらでしょうか？ 」 とかに書き直しても同じになります。

　 そこで、 問題を「 この赤玉が箱Ａ の中の赤玉である確率はいくらでしょうか？ 」 に書き換えます。

集合Ｘ ：　箱Ａ の中にある玉
集合Ｙ ：　赤色の玉

玉を１個無作為に抽出したところ、 集合Ｙ に属していたのだから、
この玉が集合Ｘ に属している確率を、次の表より求めてみましょう。



	Ｙ	Ｙ(__)
Ｘ	1/2	0
Ｘ(__)	1/4	1/4


答えは、　1/2 ÷（ 1/2 ＋ 1/4 ） ＝→　2/3　になります。


慣れてくると、次のように簡単に考えることもできるようになります。
　　　箱Ａの中に入っている赤玉を取り出す確率 ＝ 1/2 × 1 ＝→ 1/2
　　　箱Ｂの中に入っている赤玉を取り出す確率 ＝ 1/2 × 1/2 ＝→ 1/4
　　　赤玉を取り出してしまったという「 条件付き確率 」 なので、求める答えは、
　　　　　　1/2 ÷（ 1/2 ＋ 1/4 ） ＝→　2/3



プログラムによる１０万回試行のシミュレーション ：　　
　　　箱Ｂ の上の引き出しに赤玉が入っている割合 ：
　　　　　　　 %
　　　箱Ａ を抽出した割合 ：
　　　　　　　 %
　　　上の引き出しの中が赤玉だった割合 ：
　　　　　　　 %
　　　上の引き出しの中が赤玉だった場合に、 箱Ｂ の上の引き出しの中が赤玉だった割合 ：
　　　　　　　 %
　　　上の引き出しの中が赤玉だった場合に、 箱Ａ を抽出していた割合 ：
　　　　　　　 %


　　プログラムの内容 ：

（ 問題 ３ ）

　 上下２つの引き出しの付いた箱が１万個あり、 外見では区別ができません。 すべての箱は、 一方の引き出しに赤玉が１個、 他方の引き出しに白玉が１個入っています。 その中から１個を無作為に抽出し、 それを箱Ｂ と言うことにします。
　 上下２つの引き出しの付いた箱Ａ があり、 外見では箱Ｂ と区別ができません。 Ａ の箱には上下の引き出しに赤玉が１個ずつ入っています。
　 「 箱Ｂ を抽出し、 Ａ と Ｂ ２つの箱から１つを無作為に選んで上の引き出しを開けたときに赤玉が入っている。」 ということを１万回試行して調査したところ、 その割合はちょうど 3/4 でした。 箱Ｂ が決まったときに、 その上の引き出しに赤玉が入っている確率はいくらでしょうか？

（ 解答 ）

　 Ｂ の箱の上の引き出しに赤玉が入っている確率を Ｐ とする。
　 1/2 の確率でＡ の箱を選択し、 その場合は上の引き出しに赤玉が１の確率で存在する。 また、 1/2 の確率でＢ の箱を選択し、 その場合は上の引き出しに赤玉が Ｐ の確率で存在する。 したがって、 上の引き出しを開けたときに赤玉が入っている。確率は、
　　　　　1/2 ×１＋ 1/2 × Ｐ　＝→ （１＋ Ｐ ）/ 2
これが 3/4 だったのであるから、 （１＋ Ｐ ）/ 2 ＝ 3/4　よって、 Ｐ ＝ 1/2 。
よって、 答えは 1/2 です。

　 ちなみに、 上の引き出しに赤玉が入っていたとき、 箱Ａ を選択していた確率は、 次のようになります。
　　　　　（ 1/2 ×１）÷（ 1/2 ×１＋ 1/2 × Ｐ ） ＝→　1/2 ÷ 3/4　＝→　2/3 。