【 問 題 １ 】

　 ２以上の自然数 ｎ を ｍ （ ｍ は ｎ を超えない ） 個 の自然数の部分和で表します。 ただし、 同じ自然数の組み合わせでも、 足し合わせる順番が異なれば、 違った表現であるものとします。 はたしてこの表現法は何通りあるでしょうか？

　【 解 答 】

　 答えは、 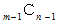です。 たとえば、 10 を ４個の自然数の部分和で表現する場合は、 全部で８４通りになります。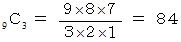
　　　　　

　 が10個あるとき、 それを４人で分配します。 １個ももらえない人はないようにします。 この時の場合の数が 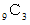になります。 その理由を考えてみましょう。

　 が10個並んでいるときに、 それを４人で分配します。 各人が順に、 楔（くさび）を１つずつ打ち込んで、 それよりも左側の をすべて獲得していきます。 最後の人は残った をすべて獲得します。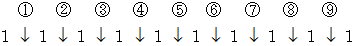

　　　　　　　　

　 その場合の数は、 ９個の楔から３個の楔を選ぶときの組み合わせの数に等しくなります。 つまり、 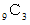になります。

【 問 題 ２ 】
　　　10個の飴玉を２人で分ける場合の数は？
　　　10個の飴玉を３人で分ける場合の数は？
　　　10個の飴玉を４人で分ける場合の数は？

　【 解 答 】

　　プログラムの内容 ：

　　　　　racさんのブログより プログラムソースをいただきました。
　　　　　　　　http://d.hatena.ne.jp/rsc96074/20120326/1332717264


【 問 題 ３ 】

　 ｎ 個 の饅頭を ｍ 人 （ ｍ は ｎ を超えない ） で分配します。 １ 個ももらえない人があってもかまいません。 全部で何通りあるでしょうか？

　【 解 答 】

　 ｎ 個 の饅頭 と ｍ−１個 の楔 の 合計 ｎ＋ｍ−１ 個 のものを １ 列に並べる場合の数が、 求める答えになります。
　　　　( ｎ＋ｍ−１ )！　÷ ｛ ｎ！ ×　( ｍ−１ )！｝

【 問 題 ４ 】

　 饅頭が１０個あります。 Ａさん から Ｊさん まで１０人います。 饅頭を分配します。 もらえない人があってもいいのですが、 もしＤさんがもらえなかったらＥさん以降の６人もすべてもらえないものとします。 分配の全ての場合の数を求めなさい。

　【 解 答 】

　　　　○ ｜ ○ ｜ ○ ｜ ○ ｜ ○ ｜ ○ ｜ ○ ｜ ○ ｜ ○ ｜ ○

　 饅頭を ○ で表します。 その間に仕切り棒を置くのですが、 それは有効にも無効にもすることができます。 有効を 1 で表し 無効を 0 で表し、 たとえば次のような場合を考えます。

　　　　○ 0 ○ 0 ○ 1 ○ 0 ○ 1 ○ 1 ○ 0 ○ 0 ○ 0 ○

　 これは、 Ａさんが３個、 Ｂさんが２個、 Ｃさんが１個、 Ｄさんが４個、 Ｅさん以降は ０ 個であることを表します。
したがって、 分配の全ての場合の数は　２⁹ ＝→　５１２ とおり で、 これが答えになります。



【 問 題 １ 】のことと併せてみると、 次の式が成り立つことが判ります。
　　　₉Ｃ₀ ＋ ₉Ｃ₁ ＋ ₉Ｃ₂ ＋ ₉Ｃ₃ ＋ ・ ・ ・ ＋ ₉Ｃ₈ ＋ ₉Ｃ₉　＝　２⁹

₉Ｃ_n ＝ ₉Ｃ_{9 −n}　ですから、 上の式は次のようになります。
　　　₉Ｃ₀ ＋ ₉Ｃ₁ ＋ ・ ・ ・ ＋ ₉Ｃ₄　＝　₉Ｃ₅ ＋ ₉Ｃ₆ ＋ ・ ・ ・ ＋ ₉Ｃ₉　＝　２⁸

一般的には、 次の式が成り立ちます。
　　　_nＣ₀ ＋ _nＣ₁ ＋ _nＣ₂ ＋ _nＣ₃ ＋ ・ ・ ・ ＋ _nＣ_{n −1} ＋ _nＣ_n　＝　２ⁿ

この式は、 次の二項展開式において、 ａ ＝ ｂ ＝ １　のときになります。
　　　

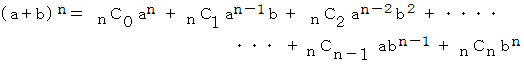
【 問 題 ５ 】

　 饅頭が10個あります。 Ａさん から Ｊさん まで10人います。 饅頭を分配します。 もらえない人があってもいいです。 ただし、 上下関係の強い集団なので、 ＢさんはＡさんよりも多くもらうことはできず、ＣさんはＢさんよりも多くもらうことはできず、 ・ ・ ・ ・ ・ 、 といったルールがあります。 分配の全ての場合の数を求めなさい。

　【 解 答 】

　 これは 「 自然数 10 の分割数を求めなさい。」 という問題です。　十進BASIC ＞ 十進BASIC＿算数 ＞ 自然数の分割 と ヤング図形　をご覧になると理由が分かるのですが、 自然数 を 個に分割する場合の数を 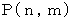とすると、 次の漸化式が成り立ちます。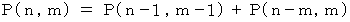
　　　　　
　 したがって、 「 自然数 の分割の方法は何通りあるか？」 という問題に答えるためには、 上記の式の を から まで １ つずつ増やしていってその総計をとります。 ｎ ＝ 10 とした次の十進BASIC のプログラムが答えを出してくれます。


プログラムの内容 ：


No. 1 ：　10　0　0　0　0　0　0　0　0　0
No. 2 ：　 9　1　0　0　0　0　0　0　0　0
No. 3 ：　 8　2　0　0　0　0　0　0　0　0
No. 4 ：　 7　3　0　0　0　0　0　0　0　0
No. 5 ：　 6　4　0　0　0　0　0　0　0　0
No. 6 ：　 5　5　0　0　0　0　0　0　0　0
No. 7 ：　 8　1　1　0　0　0　0　0　0　0
No. 8 ：　 7　2　1　0　0　0　0　0　0　0
No. 9 ：　 6　3　1　0　0　0　0　0　0　0
No.10 ：　 6　2　2　0　0　0　0　0　0　0
No.11 ：　 5　4　1　0　0　0　0　0　0　0
No.12 ：　 5　3　2　0　0　0　0　0　0　0
No.13 ：　 4　4　2　0　0　0　0　0　0　0
No.14 ：　 4　3　3　0　0　0　0　0　0　0
No.15 ：　 7　1　1　1　0　0　0　0　0　0
No.16 ：　 6　2　1　1　0　0　0　0　0　0
No.17 ：　 5　3　1　1　0　0　0　0　0　0
No.18 ：　 5　2　2　1　0　0　0　0　0　0
No.19 ：　 4　4　1　1　0　0　0　0　0　0
No.20 ：　 4　3　2　1　0　0　0　0　0　0
No.21 ：　 4　2　2　2　0　0　0　0　0　0
No.22 ：　 3　3　3　1　0　0　0　0　0　0
No.23 ：　 3　3　2　2　0　0　0　0　0　0
No.24 ：　 6　1　1　1　1　0　0　0　0　0
No.25 ：　 5　2　1　1　1　0　0　0　0　0
No.26 ：　 4　3　1　1　1　0　0　0　0　0
No.27 ：　 4　2　2　1　1　0　0　0　0　0
No.28 ：　 3　3　2　1　1　0　0　0　0　0
No.29 ：　 3　2　2　2　1　0　0　0　0　0
No.30 ：　 2　2　2　2　2　0　0　0　0　0
No.31 ：　 5　1　1　1　1　1　0　0　0　0
No.32 ：　 4　2　1　1　1　1　0　0　0　0
No.33 ：　 3　3　1　1　1　1　0　0　0　0
No.34 ：　 3　2　2　1　1　1　0　0　0　0
No.35 ：　 2　2　2　2　1　1　0　0　0　0
No.36 ：　 4　1　1　1　1　1　1　0　0　0
No.37 ：　 3　2　1　1　1　1　1　0　0　0
No.38 ：　 2　2　2　1　1　1　1　0　0　0
No.39 ：　 3　1　1　1　1　1　1　1　0　0
No.40 ：　 2　2　1　1　1　1　1　1　0　0
No.41 ：　 2　1　1　1　1　1　1　1　1　0
No.42 ：　 1　1　1　1　1　1　1　1　1　1