１次元空間と１次元時間からなる時空間で、 光の速さを とする単位系を用います。

　「 第１観察者 」は、 時空原点を通過して等速直線運動している物質を観察しています。 その物質は、 時空原点を出発して の時間後 に 空間 の位置 に存在します。 また、 物質の移動方向に第１観察者に対して速さ で移動している「 第２観察者 」がいます。 が第１観察者に対する物質の速さに等しいとき、 つまり、 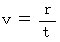のとき、 第２観察者のことを「 第０観察者 」と言うことにします。 この物質の移動を表す位置ベクトルについての 第１観察者の時空間座標系から第０観察者への時空間座標系への「 ガリレイ変換 」は次のように表されます。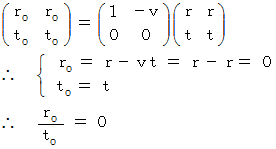

　　　　　
　 しかし、 実験より 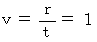の電磁波の伝わる速さに関しては、 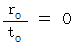ではなく、 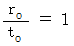となることが解りました。 そこでアインシュタインはこう考えたのです。
　　　　「 時空間の中での、 電磁波の伝わり方と 物質の移動 は 同じ形式をとる。」

　 これは、 実験では確かめられていませんでしたので、 あくまでも仮定です。 その仮定の上に、 彼は次のように考えたのです。
　　　　「 現実は、 ガリレイ変換ではない新たな座標変換を必要とする。」

以上の２つの考えを結びつけたのが、 次のアイディアでした。
　　　　「 電磁波の伝わり方も 物質の移動 も、 次の条件を満たす座標変換に従う。
　　　　　　　　　　　　　　　　　　」

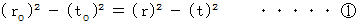前述のとおり、 電磁波の伝わり方については、 実験で次のことが確かめられていました。
　　　　
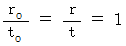
　 ですから、 電磁波の伝わり方については が確かに成り立ちます。 逆に言えば、 電磁波の伝わり方が に従うので、 物質の時空間内移動形式も に従うであろうと仮定したわけです。 そうして、 この条件を満たす座標変換は、「 ローレンツ変換 」という直交座標系を斜交座標系へと変換するものであることを見抜いて、 彼をそれを相対性理論に採用したのです。

ローレンツ変換による、 第１観察者 から 第０観察者 への座標変換は次のように表されます。
　　　　
　　　　

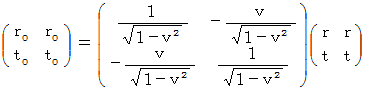
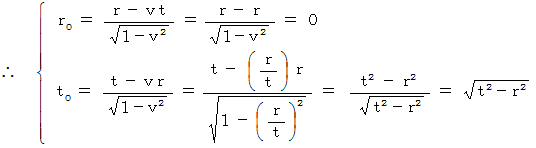
　 上の式から、 物質の移動については、 が成り立つことがわかります。 相対的な速さ で等速直線運動をしている２人の観察者がいて、 お互いが２人の時空間移動を観察しているときに、 ２人の関係は、「 第１観察者 と 第０観察者 との関係 」であり、 かつ、「 第０観察者 と 第１観察者 との関係 」ですから、 が成り立っていることは矛盾になります。 このように、 以上の仮定の上に成り立っている現在の相対性理論からは、 様々な論理的矛盾が導かれます。 そこで、 アインシュタインの仮定を修正してやる必要があります。 しかし、 時間を虚数とすれば解決できる論理的矛盾もあり、 完全否定ではなく「 失敗は成功の母 」となるように考えていけば、 物質の移動 と 波の伝播 の様式が結びつくのかもしれません。