1000人の100点満点の数学のテストの得点からなる母集団があります。 次の式たちを使って、 各人の得点の偏差値を求めて、 国語のテストの偏差値と比較します。

　　　　
　　　　
　　　　

　 さて、 標準偏差が偏差の２乗の平均の平方根の正の値を用いる理由はなんでしょうか？　「 標準偏差は、 偏差の絶対値の平均（ 平均絶対偏差 ）である。」 と定義してもよいのではないでしょうか？　それのほうが簡単ですし ・ ・ ・ ・ 。
　　　　
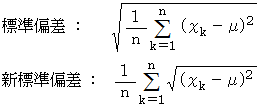
　 たとえば、母集団が、 −２点が１個、 −１点が２個、 ０点が３個、 ＋１点が２個、 ＋２点が１個　ならば、 次のようになります。
　　　　

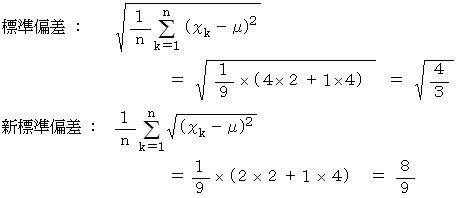
　 しかし、 こうならないのには理由があります。 それは正規分布です。 正規分布は確率分布の一種です。
　　　
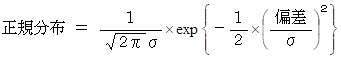
この式があるため、 標準偏差 （ σ ） は 「 偏差の２乗の平均（ 分散 σ² ）の平方根の正の値 」 になっているのです。


もし、 分布が正規分布である場合は、 次のようになります。
　　　　　偏差値 60以上の者は、 全体の 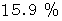存在する。
　　　　　偏差値 70以上の者は、 全体の 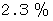存在する。
　　　　　偏差値 80以上の者は、 全体の 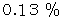存在する。


平均値 、 標準偏差 の 標準正規分布は、 次の方程式で表されます。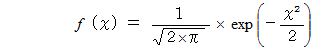


最後に、 次の方程式を表す図を示します。
　　　　　　　

　　　　

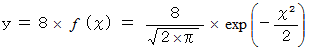
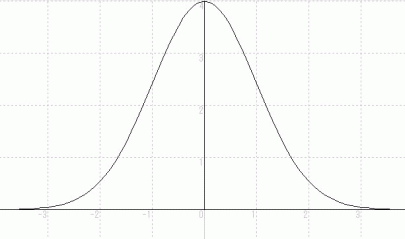
追伸 ：

　　確率変数は、 偏差が大きいほどバラツキの度合いを累乗的に大きくする因子になります。
　　
　　標準偏差は　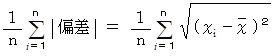　ではありません。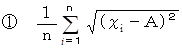
　　
　　
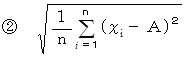
　　 は　Ａ ＝ 中央値 のときに最小になります。
　　 は　Ａ ＝ 平均値 のときに最小になります。
　　 は　Ａ ＝ 平均値 のとき、 標準偏差になります。


「 分散 」と「 標準偏差 」と「平均絶対偏差」との違いの例：

Ａ群 も Ｂ群 も　標本数 10個　平均 50
　　　Ａ群：　50　50　55　45　60　40　65　35　70　30
　　　Ｂ群：　50　50　60　40　70　30　80　20　90　10

Ａ群の分散：　( 2×0 ＋ 2×25 ＋ 2×100 ＋ 2×225 ＋ 2×400 ) ÷ 10　＝→　150
Ｂ群の分散：　( 2×0 ＋ 2×100 ＋ 2×400 ＋ 2×900 ＋ 2×1600 ) ÷ 10　＝→　600
Ａ群の分散 の Ｂ群の分散 に対する比率：　0.25

Ａ群の標準偏差：　ルート(150) ≒→ 12.2
Ｂ群の標準偏差：　ルート(600) ≒→ 24.5
Ａ群の標準偏差 の Ｂ群の標準偏差 に対する比率：　0.49795918…

Ａ群の平均絶対偏差：　( 2×0 ＋ 2×5 ＋ 2×10 ＋ 2×15 ＋ 2×20 ) ÷ 10　＝→　10
Ｂ群の平均絶対偏差：　( 2×0 ＋ 2×10 ＋ 2×20 ＋ 2×30 ＋ 2×40 ) ÷ 10　＝→　20
Ａ群の平均絶対偏差 の Ｂ群の平均絶対偏差 に対する比率：　0.5