(1) ガウス積分
-
極座標変換を用いて、 次のガウス積分の式が成り立つことを証明しましょう。
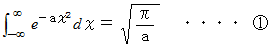
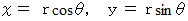 によって、 極座標系から直交座標系に変換されるものとします。
によって、 極座標系から直交座標系に変換されるものとします。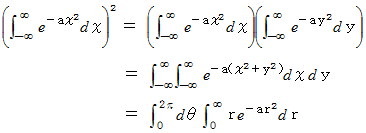
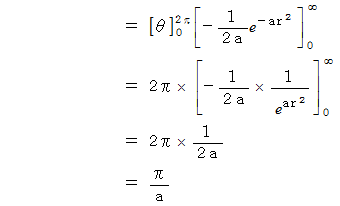

-
最も頻度の多い確率分布といえば、 正規分布です。 平均を
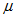 、 分散を
、 分散を 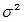 としますと、 正規分布は次の式で表されます。
としますと、 正規分布は次の式で表されます。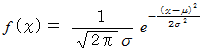
これから、
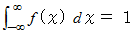 になっていることを証明してみましょう。
になっていることを証明してみましょう。
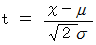 とおくと、
とおくと、したがって、

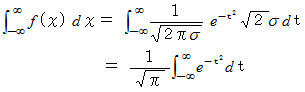
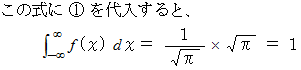
したがって、 正規分布曲線 と
 軸 とで囲まれる範囲の面積は
軸 とで囲まれる範囲の面積は  です。
です。 統計学 へ戻る
統計学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る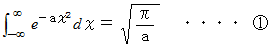
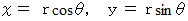 によって、 極座標系から直交座標系に変換されるものとします。
によって、 極座標系から直交座標系に変換されるものとします。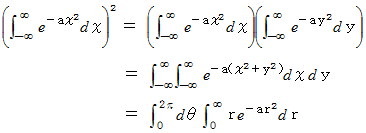
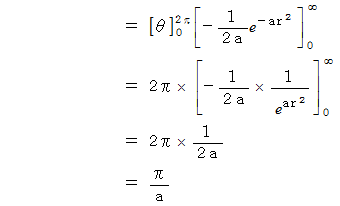

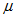 、 分散を
、 分散を 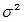 としますと、 正規分布は次の式で表されます。
としますと、 正規分布は次の式で表されます。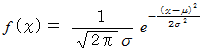
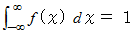 になっていることを証明してみましょう。
になっていることを証明してみましょう。
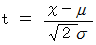 とおくと、
とおくと、
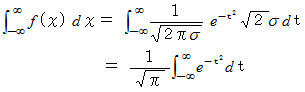
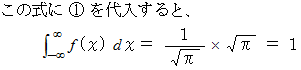
 軸 とで囲まれる範囲の面積は
軸 とで囲まれる範囲の面積は  です。
です。