 今回は、 簡明化のために、 積分で現れる定数
今回は、 簡明化のために、 積分で現れる定数 を省略しています。
を省略しています。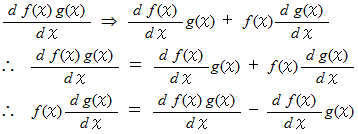
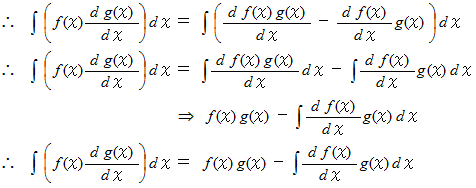
上の式が部分積分の公式です。
部分積分法の例として、
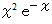 を積分してみましょう。
を積分してみましょう。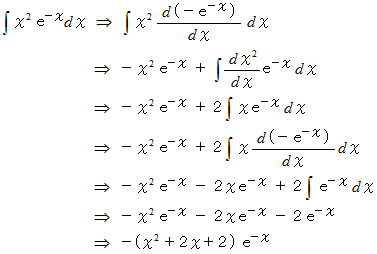
【 問 題 1 】
-
積分定数を C として、 x2 sin x の不定積分を求めよ。
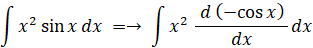
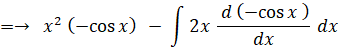
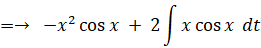
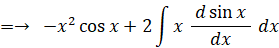
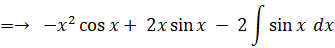
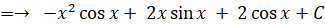
-
積分定数を C として、( log x ) 2 の不定積分を求めよ。
-
t = log x と置く
x = e t
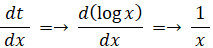
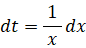
d x = x d t =→ e t d t
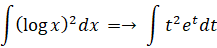
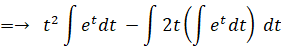 ← 部分積分
← 部分積分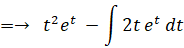
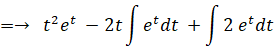
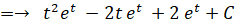
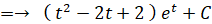
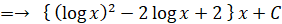
-
積分定数を C = 0 として、 次の不定積分を求めよ。
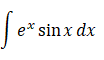
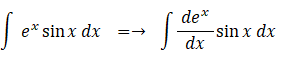
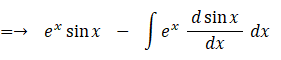
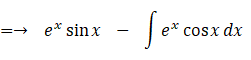
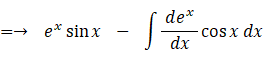
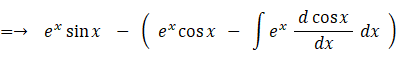
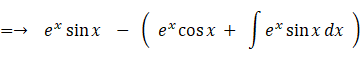
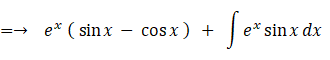
したがって、
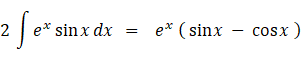
よって、
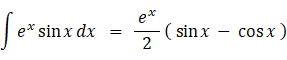
 解析学 へ戻る
解析学 へ戻る