(1) 物理学的空間( 2次元空間 )
-
点
 は、 時刻
は、 時刻  のときに原点にあり、 経過とともに変位します。 時刻
のときに原点にあり、 経過とともに変位します。 時刻  のときの点
のときの点 の位置ベクトル
の位置ベクトル 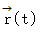 は、次のように表されるものとします。
は、次のように表されるものとします。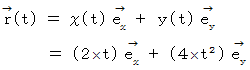
グラフ 1
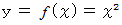
すると、 時刻
 のときの点
のときの点 の速度
の速度 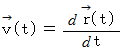 は、 次のように表されます。
は、 次のように表されます。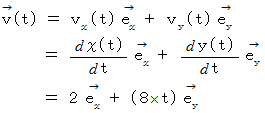
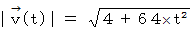
また、 時刻
 までに点
までに点 が移動した道のりは次のように表されます。
が移動した道のりは次のように表されます。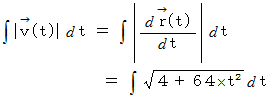
コメント :
点
 のような一方方向への移動の場合は、 これでいいのですが、 たとえば次のよ
のような一方方向への移動の場合は、 これでいいのですが、 たとえば次のような周期運動の場合は 、道のりは
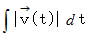 からは求めることはできません。
からは求めることはできません。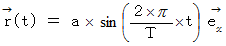
この場合、 時刻
 における道のりは
における道のりは  なのですが、 この式によると
なのですが、 この式によると  に
になってしまいます。
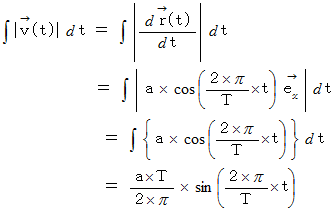
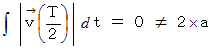
-
先ほどの点
 の移動について、
の移動について、  軸の1次元空間のみを考えることにします。 つまり、
軸の1次元空間のみを考えることにします。 つまり、  軸方向の速さは
軸方向の速さは  として考えます。
として考えます。時刻
 のときの点
のときの点 の位置は、 次のように表されます。
の位置は、 次のように表されます。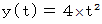
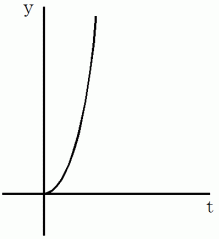
グラフ 2 ( これは 空間 ではなく、 時空間 のグラフです。)
時刻
 のときの点
のときの点 の
の 軸方向への速さは、 次のように表されます。
軸方向への速さは、 次のように表されます。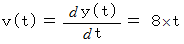
グラフ 3 ( これは 空間 でも 時空間 でもありません。 相関関係のグラフです。)
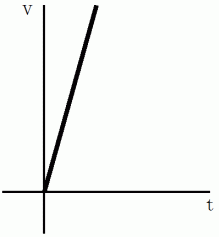
時刻
 までの点
までの点 の道のりは、 次のように表されます。 これは点
の道のりは、 次のように表されます。 これは点 の位置に等しいです。
の位置に等しいです。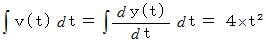
-
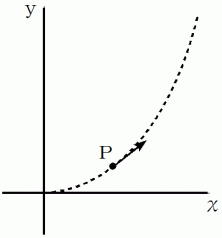
グラフ 4 は、 点
 の軌跡を表したグラフです。
の軌跡を表したグラフです。グラフ 4
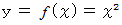
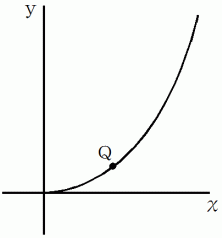
点
 の位置ベクトル
の位置ベクトル 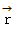 は、 次のように表されます。
は、 次のように表されます。
原点から点
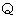 までの曲線の長さは、 次のように表されます。
までの曲線の長さは、 次のように表されます。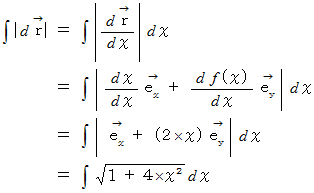
ちなみに、 この式で
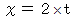 と置くと、 次のようになります。
と置くと、 次のようになります。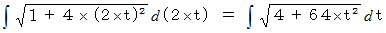
このように曲線が
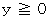 の領域にあるとき、 次の4つの線分で囲まれる部分の面積は、 次のようになります。
の領域にあるとき、 次の4つの線分で囲まれる部分の面積は、 次のようになります。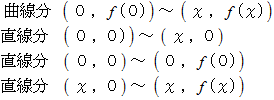
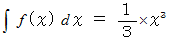
 解析学 へ戻る
解析学 へ戻る