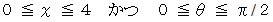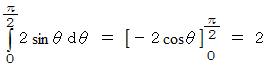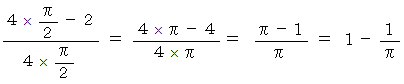落下位置の確率 ( ビュフォンの針 )
 確率 へ戻る
確率 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2012.08.04____
落下傘で降下したりウィングスーツで滑空したりする人は、 たいしたもんだと思います。 怖さ知らずに飛び降りて、 自分の意図する所へ着地することができるのです。 物質を落下させて平地の上で最終的に静止する位置を予想することは困難ですが、 決められたエリアに入ることを確率的に予想することはできます。
( 問題 1 )
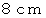 四方の格子が描かれた平らな床の上から、 直径
四方の格子が描かれた平らな床の上から、 直径 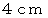 の円盤を落とします。 落とされた円盤が静止した時に、 格子の交点の上に存在する確率はいくらでしょうか?
の円盤を落とします。 落とされた円盤が静止した時に、 格子の交点の上に存在する確率はいくらでしょうか?
( 解答 )
円盤の中心が下図の円の中に存在するときだけ、 円盤が格子の交点の上に存在することになりますので、 その面積の合計の全体の面積に対する比が、 求める確率になります。というのも、 落とされて静止した円盤の中心が存在する確率は、 床上の点ではどこも同じと考えてよいからです。
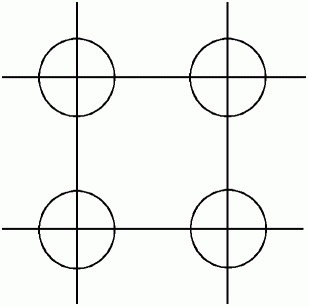
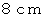 四方の正方形の部分に注目します。 この中で円に含まれる部分の割合は次のようになります。
四方の正方形の部分に注目します。 この中で円に含まれる部分の割合は次のようになります。
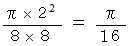
隣の正方形についても同様のことが言えますので、 マクロ的にみても面積の割合はこれと同じになると言えます。 したがって、 求める確率は次のようになります。
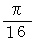
もし、 この実験を1000回行って、 落とされた円盤が静止した時に格子の交点の上に存在する実験的確率が  であった場合、 次の式から
であった場合、 次の式から  の値を推測することができます。
の値を推測することができます。
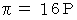
( 問題 2 )
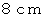 四方の格子が描かれた平らな床の上から、 直径
四方の格子が描かれた平らな床の上から、 直径 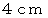 の円盤を落とします。 落とされた円盤が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
の円盤を落とします。 落とされた円盤が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
( 解答 )
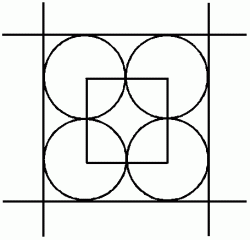
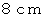 四方の正方形の部分に注目します。 円盤の中心が上図の小さな正方形の中に存在するときだけ、 円盤が格子に接触しないことになりますので、 小さな正方形の面積の大きな正方形の面積に対する比が、 求める確率になります。
四方の正方形の部分に注目します。 円盤の中心が上図の小さな正方形の中に存在するときだけ、 円盤が格子に接触しないことになりますので、 小さな正方形の面積の大きな正方形の面積に対する比が、 求める確率になります。
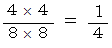
( 問題 3 )
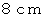 四方の格子が描かれた平らな床の上から、 長さ
四方の格子が描かれた平らな床の上から、 長さ 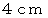 の針金を落とします。 落とされた針金が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
の針金を落とします。 落とされた針金が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
( 解答 )
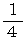 よりも大きいことは解りますが、 それ以上のことは今の私にはわかりません。
よりも大きいことは解りますが、 それ以上のことは今の私にはわかりません。
これに似た問題が、 18世紀のイギリスの数学者ビュフォンによって提出され、 その解答も与えられました。
( 問題 4 : 「 ビュフォンの針 」 の問題の簡単なケース )
長さ 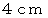 の針金を間隔
の針金を間隔 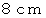 の無数の平行線の上に落としたとき、 針金が線に全く接触しない確率はいくらになるでしょうか?
の無数の平行線の上に落としたとき、 針金が線に全く接触しない確率はいくらになるでしょうか?
( 解答 )
針金の中心から最も近い直線までの距離を 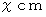 とし、 針金とその直線のなす鋭角を
とし、 針金とその直線のなす鋭角を  とします。 すると次の範囲になります。
とします。 すると次の範囲になります。
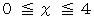
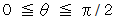
そして、  も
も  もこの範囲の中で、 まんべんなく いろんな値を取ります。
もこの範囲の中で、 まんべんなく いろんな値を取ります。
針金が直線に接触する条件は次のようになります。
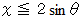
横軸に  、 縦軸に
、 縦軸に  をとりますと、
をとりますと、 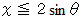 は次のグラフの灰色の部分になります。
は次のグラフの灰色の部分になります。
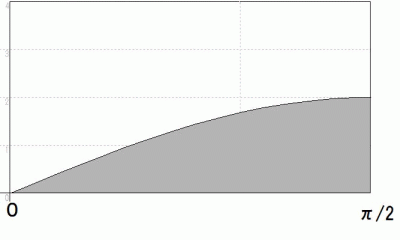
したがって、 求める確率は、 下の部分で示される長方形の面積に対する、
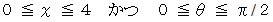
灰色ではない部分の面積の比になります。
灰色の部分の面積は次のようになります。
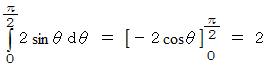
したがって、 求める答えは次のようになります。
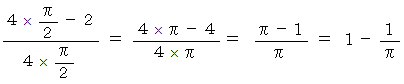
参考: 大学生のための数学 > プログラミング > モンテカルロ法
 確率 へ戻る
確率 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る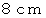 四方の格子が描かれた平らな床の上から、 直径
四方の格子が描かれた平らな床の上から、 直径 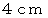 の円盤を落とします。 落とされた円盤が静止した時に、 格子の交点の上に存在する確率はいくらでしょうか?
の円盤を落とします。 落とされた円盤が静止した時に、 格子の交点の上に存在する確率はいくらでしょうか?
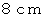 四方の正方形の部分に注目します。 この中で円に含まれる部分の割合は次のようになります。
四方の正方形の部分に注目します。 この中で円に含まれる部分の割合は次のようになります。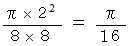
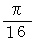
 であった場合、 次の式から
であった場合、 次の式から  の値を推測することができます。
の値を推測することができます。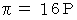
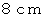 四方の格子が描かれた平らな床の上から、 直径
四方の格子が描かれた平らな床の上から、 直径 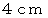 の円盤を落とします。 落とされた円盤が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
の円盤を落とします。 落とされた円盤が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
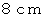 四方の正方形の部分に注目します。 円盤の中心が上図の小さな正方形の中に存在するときだけ、 円盤が格子に接触しないことになりますので、 小さな正方形の面積の大きな正方形の面積に対する比が、 求める確率になります。
四方の正方形の部分に注目します。 円盤の中心が上図の小さな正方形の中に存在するときだけ、 円盤が格子に接触しないことになりますので、 小さな正方形の面積の大きな正方形の面積に対する比が、 求める確率になります。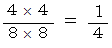
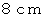 四方の格子が描かれた平らな床の上から、 長さ
四方の格子が描かれた平らな床の上から、 長さ 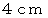 の針金を落とします。 落とされた針金が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?
の針金を落とします。 落とされた針金が静止した時に、 格子に接触しないで存在する確率はいくらでしょうか?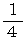 よりも大きいことは解りますが、 それ以上のことは今の私にはわかりません。
よりも大きいことは解りますが、 それ以上のことは今の私にはわかりません。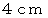 の針金を間隔
の針金を間隔 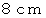 の無数の平行線の上に落としたとき、 針金が線に全く接触しない確率はいくらになるでしょうか?
の無数の平行線の上に落としたとき、 針金が線に全く接触しない確率はいくらになるでしょうか?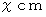 とし、 針金とその直線のなす鋭角を
とし、 針金とその直線のなす鋭角を  とします。 すると次の範囲になります。
とします。 すると次の範囲になります。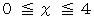
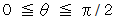
 も
も  もこの範囲の中で、 まんべんなく いろんな値を取ります。
もこの範囲の中で、 まんべんなく いろんな値を取ります。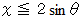
 、 縦軸に
、 縦軸に  をとりますと、
をとりますと、 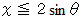 は次のグラフの灰色の部分になります。
は次のグラフの灰色の部分になります。