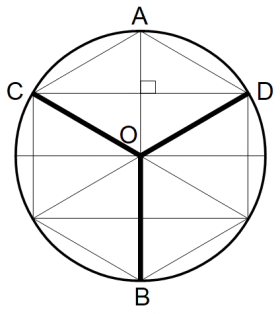
分度器を用いないでケーキを３人で均等に分けるには、次のような方法があります。まず、ケーキの表面に直径ＡＢを引きます。次に直径の一端から直径の 1/4 の長さ内側にその直径に垂直な直線（ＣＤ）を引きます。ケーキの中心をＯとすると、ＯＢ と ＯＣ と ＯＤ でカットすると、合同なケーキが３ピースできます。

　　　　


　分度器を用いないでケーキを３人で均等に分けるには、次のような方法もあります。ケーキの直径を１とすると、直径の両端から 0.3675 の長さ内側にその直径に対して垂直に切断してケーキを３つに分ける方法です。

【 問 題 】

半径１（ 直径２ ）の半円があり、灰色の部分は半円の面積の 1/3 を占める。
　　　
　　

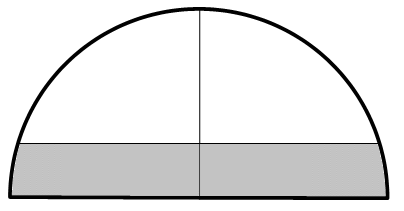
ＣＰの長さの近似値を小数点以下３桁で求めよ。

【 解 答 】

∠ＥＯＡ ＝ ∠ＤＯＢ ＝ θ　とする。
ＯＰ ＝ x　とする。
ＯＰ ＝ sin θ ＝ x　　⇔　　θ ＝ Arcsin x
ＥＰ ＝ cos θ　＝　ルート( 1−x² )
灰色の部分の面積は、△ＯＤＥの面積に弧ＯＡＥの面積の２倍を加えたものである。
△ＯＤＥ ＝ 1/2 × ＥＤ × ＯＰ ＝→　x cos θ　＝→　x ルート( 1−x² )
弧ＯＡＥ ＝ π/2 × θ/π　＝→　θ/2　＝→　Arcsin x / 2
したがって、灰色の部分の面積は、x ルート( 1−x² ) ＋ Arcsin x
これが、半円の面積 π/2 の 1/3 になるような x の近似値を次の十進BASICのプログラムを実行して求める。

　　　PRINT
　　　PRINT "π/6 ＝ "; PI/6
　　　PRINT
　　　FOR x=0.26 TO 0.27 STEP 0.001
　　　PRINT x; " :　"; x_*SQR(1−x^2)+ASIN(x)
　　　NEXT x
　　　END

これを実行すると、次のようにアウトプット表示される。

　　　π/6 ＝　.523598775598299
　　 　.26　:　 .514080443163594
　　　.261　:　 .516011390765783
　　　.262　:　 .517941797625022
　　　.263　:　 .519871661517114
　　　.264　:　 .52180098021598
　　　.265　:　 .523729751493657
　　　.266　:　 .525657973120283
　　　.267　:　 .527585642864089
　　　.268　:　 .529512758491387
　　　.269　:　 .531439317766563
　　 　.27　:　 .533365318452067

よって、x ≒ 0.265　となる。
したがって、答えは　1−0.265 ＝→ 0.735　となる。