傗傗偙偟傗忦審晅偒妋棪
 妋棪 傊栠傞
妋棪 傊栠傞
 戝妛惗偺偨傔偺悢妛 傊栠傞
戝妛惗偺偨傔偺悢妛 傊栠傞
2021.01.27____
亂 栤 戣 亃
丂僕儑乕僇乕傪彍偄偨 52 枃偺僩儔儞僾僇乕僪偺拞偐傜柍嶌堊偵 4 枃傪慖傃傑偡丅偦偺拞偐傜柍嶌堊偵俁枃傪慖傫偱挷傋偨偲偙傠丄俁枃偲傕僟僀傾偺僇乕僪偱偟偨丅巆傞侾枃傕僟僀傾偱偁傞妋棪偼偄偔傜偱偟傚偆偐丠
亂 夝 摎 亃
52枃偺僇乕僪偐傜4枃傪柍嶌堊偵拪弌偟偨偲偒丄4枃偲傕僟僀儎偺僇乕僪偱偁傞妋棪丗
丂丂丂13/52 亊 12/51 亊 11/50 亊 10/49丂亖仺丂( 13丒12丒11丒10 ) / ( 52丒51丒50丒49 )丂丂丒丒丒 嘆
52枃偺僇乕僪偐傜4枃傪柍嶌堊偵拪弌偟偨偲偒丄3枃僟僀儎偺僇乕僪偱偁傞妋棪丗
丂丂丂( 13俠3 亊 39俠1 ) 亊 4俹4 亐 52俹4丂亖仺丂( 13丒12丒11丒39丒4 ) / ( 52丒51丒50丒49 )丂丂丒丒丒 嘇
4枃偲傕僟僀儎偺僇乕僪偱偁傞4枃偺僇乕僪偐傜3枃偺僇乕僪傪拪弌偟偨偲偒丄3枃偲傕僟僀儎偺僇乕僪偱偁傞妋棪丗
丂丂丂1丂丂丒丒丒 嘊
3枃偑僟僀儎偺僇乕僪偱偁傞4枃偺僇乕僪偐傜3枃偺僇乕僪傪拪弌偟偨偲偒丄3枃偲傕僟僀儎偺僇乕僪偱偁傞妋棪丗
丂丂丂3/4 亊 2/3 亊 1/2丂亖仺丂1/4丂丂丒丒丒 嘋
忦審晅偒妋棪傛傝摎偊傪媮傔傞丗
丂丂丂( 嘆亊嘊 ) 亐 ( 嘆亊嘊 亄 嘇亊嘋 )
丂丂丂丂丂丂亖仺丂( 13丒12丒11丒10 ) / ( 52丒51丒50丒49 ) 亐乷 ( 13丒12丒11丒10 ) / ( 52丒51丒50丒49 ) 亄 ( 13丒12丒11丒39丒4 ) / ( 52丒51丒50丒49丒4 ) 乸
丂丂丂丂丂丂亖仺丂( 13丒12丒11丒10丒4 ) / ( 52丒51丒50丒49丒4 ) 亐 [乷 ( 13丒12丒11丒10丒4 ) 亄 ( 13丒12丒11丒39丒4 ) 乸/ ( 52丒51丒50丒49丒4 ) ]
丂丂丂丂丂丂亖仺丂( 13丒12丒11丒10丒4 ) 亐乷 ( 13丒12丒11丒10丒4 ) 亄 ( 13丒12丒11丒39丒4 ) 乸
丂丂丂丂丂丂亖仺丂( 13丒12丒11丒10丒4 ) 亐乷 ( 13丒12丒11丒4 ) 亊 ( 10 亄 39) 乸
丂丂丂丂丂丂亖仺丂10 亐 ( 10 亄 39) 乸
丂丂丂丂丂丂亖仺丂10 / 49丂佮仺丂20.4 %
亂 暿 夝 亃
忦審晅偒妋棪傛傝
丂丂丂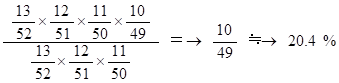
慡懱偐傜傑偢倣屄傪拪弌偟丄偦偺倣屄偺拞偐傜値屄傪拪弌偡傞偙偲偼丄慡懱偐傜値屄傪拪弌偡傞偙偲偵摍偟偄偺偱偡丅
亂 暿 夝 亃
丂寢嬊丄52 枃偺僇乕僪偐傜3枃偺僟僀傾偺僇乕僪傪彍偄偨傕偺偺拞偐傜 1 枃傪慖傫偱偄偨偙偲偱偁傞偐傜丄偦偺妋棪偼 10/49 偱 栺 20.4 % 偱偁傞丅偙偺栤戣偼丄忦審晅偒妋棪傪抦傜側偄恖偺曽偑娙扨偐傕偟傟傑偣傫丅抦幆昻朢偲偼偙偺偙偲側傝丅
 妋棪 傊栠傞
妋棪 傊栠傞 戝妛惗偺偨傔偺悢妛 傊栠傞
戝妛惗偺偨傔偺悢妛 傊栠傞