位の数がすべて異なる確率
 確率 へ戻る
確率 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2014.09.27
A君とBさんは相談することなく 1 から 5 の5個の自然数をすべて使って5桁の数を作ります。 そしてその数を提示し合って、 それぞれの位の数を比較します。 このとき、 位の数が少なくとも1組以上同じになる確率はいくらでしょうか?
(0) 誤解答
A君は必ず少ない数の順に並べるというこだわりを持っていて、 12345 という数を作り、 Bさんはランダムな数を作るとします。 このケースについて確率を求めても、 この問題の求める確率と同じです。 したがって答えは次のようになると考えられます。
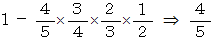
しかし、 この答えは間違っています 。 もし、 この問題が 「 A君は 1 から 5 の5枚のカードの中から、 Bさんに解らないように 1 枚を選んで裏返しに置き、 そのカードをBさんに当ててもらいます。 正解かどうかカードを表にして確かめます。 それが終わったら、 同様にして次のカードをBさんに当ててもらいます。 こうしてすべてのカードについてBさんが予想をした時、 2回以上当たる確率はいくらでしょうか? 」 という問題ならこの答えでいいのですが。
さて、 この問題で、 たとえばBさんが 31254 という数を作ったとしましょう。 2つの数の万の位の数が一致しない確率は 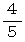 であり、 Bさんは 3 を選んだわけですから、 2つの数のすべての位の数が一致しないための必要条件の1つをクリアしています。 それがクリアされた後、 千の位が一致しない確率は、 Bさんが 1 と 2 と 4 と 5 の4個の数から2以外の数を選ぶ確率になっているので、 確率は
であり、 Bさんは 3 を選んだわけですから、 2つの数のすべての位の数が一致しないための必要条件の1つをクリアしています。 それがクリアされた後、 千の位が一致しない確率は、 Bさんが 1 と 2 と 4 と 5 の4個の数から2以外の数を選ぶ確率になっているので、 確率は 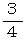 になります。 Bさんは 1 を選んだわけですから、 2つの数のすべての位の数が一致しないための2つ目の必要条件をクリアしています。 それがクリアされた後、 百の位が一致しない確率は、 Bさんが 2 と 5 と 4 の3個の数から3以外の数を選ぶ確率になっているので、 確率は
になります。 Bさんは 1 を選んだわけですから、 2つの数のすべての位の数が一致しないための2つ目の必要条件をクリアしています。 それがクリアされた後、 百の位が一致しない確率は、 Bさんが 2 と 5 と 4 の3個の数から3以外の数を選ぶ確率になっているので、 確率は 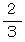 ではなくて
ではなくて  になります。 Bさんは 2 を選んだわけですから、 2つの数のすべての位の数が一致しないための3つ目の必要条件をクリアしています。 それがクリアされた後、 十の位が一致しない確率は、 Bさんが 4 と 5 の2個の数から4以外の数を選ぶ確率になっているので、 確率は
になります。 Bさんは 2 を選んだわけですから、 2つの数のすべての位の数が一致しないための3つ目の必要条件をクリアしています。 それがクリアされた後、 十の位が一致しない確率は、 Bさんが 4 と 5 の2個の数から4以外の数を選ぶ確率になっているので、 確率は 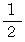 になります。 Bさんは 5 を選んだわけですから、 2つの数のすべての位の数が一致しないための4つ目の必要条件をクリアしています。 このように具体的にみていきますと、 この答えは間違っていることが解ります。 また、次のシミュレーションをみてもこれが誤解答であるっことは明らかです。
になります。 Bさんは 5 を選んだわけですから、 2つの数のすべての位の数が一致しないための4つ目の必要条件をクリアしています。 このように具体的にみていきますと、 この答えは間違っていることが解ります。 また、次のシミュレーションをみてもこれが誤解答であるっことは明らかです。
(1) プログラムによる「 モンモールの出合いの問題 」のシミュレーション
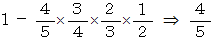
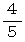 であり、 Bさんは 3 を選んだわけですから、 2つの数のすべての位の数が一致しないための必要条件の1つをクリアしています。 それがクリアされた後、 千の位が一致しない確率は、 Bさんが 1 と 2 と 4 と 5 の4個の数から2以外の数を選ぶ確率になっているので、 確率は
であり、 Bさんは 3 を選んだわけですから、 2つの数のすべての位の数が一致しないための必要条件の1つをクリアしています。 それがクリアされた後、 千の位が一致しない確率は、 Bさんが 1 と 2 と 4 と 5 の4個の数から2以外の数を選ぶ確率になっているので、 確率は 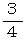 になります。 Bさんは 1 を選んだわけですから、 2つの数のすべての位の数が一致しないための2つ目の必要条件をクリアしています。 それがクリアされた後、 百の位が一致しない確率は、 Bさんが 2 と 5 と 4 の3個の数から3以外の数を選ぶ確率になっているので、 確率は
になります。 Bさんは 1 を選んだわけですから、 2つの数のすべての位の数が一致しないための2つ目の必要条件をクリアしています。 それがクリアされた後、 百の位が一致しない確率は、 Bさんが 2 と 5 と 4 の3個の数から3以外の数を選ぶ確率になっているので、 確率は 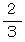 ではなくて
ではなくて  になります。 Bさんは 2 を選んだわけですから、 2つの数のすべての位の数が一致しないための3つ目の必要条件をクリアしています。 それがクリアされた後、 十の位が一致しない確率は、 Bさんが 4 と 5 の2個の数から4以外の数を選ぶ確率になっているので、 確率は
になります。 Bさんは 2 を選んだわけですから、 2つの数のすべての位の数が一致しないための3つ目の必要条件をクリアしています。 それがクリアされた後、 十の位が一致しない確率は、 Bさんが 4 と 5 の2個の数から4以外の数を選ぶ確率になっているので、 確率は 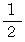 になります。 Bさんは 5 を選んだわけですから、 2つの数のすべての位の数が一致しないための4つ目の必要条件をクリアしています。 このように具体的にみていきますと、 この答えは間違っていることが解ります。 また、次のシミュレーションをみてもこれが誤解答であるっことは明らかです。
になります。 Bさんは 5 を選んだわけですから、 2つの数のすべての位の数が一致しないための4つ目の必要条件をクリアしています。 このように具体的にみていきますと、 この答えは間違っていることが解ります。 また、次のシミュレーションをみてもこれが誤解答であるっことは明らかです。 確率 へ戻る
確率 へ戻る