【 問 題 1 】
-
サイコロを繰り返し振ったときに 1,2,3,4,5,6 のパターンが出現するためには、平均して何回サイコロを振らなけばならないか?
-
目的のパターンになることを念願成就と言うことにする。
念願成就できるために平均して何回サイコロを振らなければならないか、その期待値を f(E0) とする。
f(E1) : 1 が出た直後にあと何回で念願成就できるかの期待値
f(E2) : 1,2 と出た直後にあと何回で念願成就できるかの期待値
f(E3) : 1,2,3 と出た直後にあと何回で念願成就できるかの期待値
f(E4) : 1,2,3,4 と出た直後にあと何回で念願成就できるかの期待値
f(E5) : 1,2,3,4,5 と出た直後にあと何回で念願成就できるかの期待値
 : f(E0) = 1/6 × ( 1 + f(E1) ) + 5/6 × ( 1 + f(E0) )
: f(E0) = 1/6 × ( 1 + f(E1) ) + 5/6 × ( 1 + f(E0) ) : f(E1) = 1/6 × ( 1 + f(E2) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E1) = 1/6 × ( 1 + f(E2) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E2) = 1/6 × ( 1 + f(E3) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E2) = 1/6 × ( 1 + f(E3) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E3) = 1/6 × ( 1 + f(E4) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E3) = 1/6 × ( 1 + f(E4) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E4) = 1/6 × ( 1 + f(E5) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E4) = 1/6 × ( 1 + f(E5) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E5) = 1/6 × 1 + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E5) = 1/6 × 1 + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )よって、
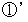 : f(E0) = f(E1) + 6 ・・・
: f(E0) = f(E1) + 6 ・・・ 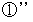
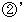 : 4f(E0) - 5f(E1) + f(E2) + 6 = 0
: 4f(E0) - 5f(E1) + f(E2) + 6 = 0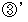 : 4f(E0) + f(E1) - 6f(E2) + f(E3) + 6 = 0
: 4f(E0) + f(E1) - 6f(E2) + f(E3) + 6 = 0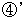 : 4f(E0) + f(E1) - 6f(E3) + f(E4) + 6 = 0
: 4f(E0) + f(E1) - 6f(E3) + f(E4) + 6 = 0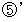 : 4f(E0) + f(E1) - 6f(E4) + f(E5) + 6 = 0
: 4f(E0) + f(E1) - 6f(E4) + f(E5) + 6 = 0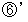 : 4f(E0) + f(E1) - 6f(E5) + 6 = 0
: 4f(E0) + f(E1) - 6f(E5) + 6 = 0 →
→  にて、
にて、f(E2) = f(E1) - 30 ・・・
 &
&  →
→  にて、
にて、f(E3) = f(E1) - 210 ・・・
 &
&  →
→ 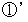 にて、
にて、f(E4) = f(E1) - 1290 ・・・ ④”
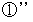 & ④”→
& ④”→ 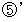 にて、
にて、f(E5) = f(E1) - 7770 ・・・

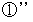 &
&  →
→ 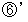 にて、
にて、f(E1) = 46650 ・・・ ⑥”
⑥” →
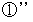 にて、
にて、f(E0) = 46656 =→ 66
したがって答えは、 46656 回
-
サイコロを繰り返し振ったときに 1,2,3,4,5,1 のパターンが出現するためには、平均して何回サイコロを振らなけばならないか?
-
目的のパターンになることを念願成就と言うことにする。
念願成就できるために平均して何回サイコロを振らなければならないか、その期待値を f(E0) とする。
f(E1) : 1 が出た直後にあと何回で念願成就できるかの期待値
f(E2) : 1,2 と出た直後にあと何回で念願成就できるかの期待値
f(E3) : 1,2,3 と出た直後にあと何回で念願成就できるかの期待値
f(E4) : 1,2,3,4 と出た直後にあと何回で念願成就できるかの期待値
f(E5) : 1,2,3,4,5 と出た直後にあと何回で念願成就できるかの期待値
 : f(E0) = 1/6 × ( 1 + f(E1) ) + 5/6 × ( 1 + f(E0) )
: f(E0) = 1/6 × ( 1 + f(E1) ) + 5/6 × ( 1 + f(E0) ) : f(E1) = 1/6 × ( 1 + f(E2) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E1) = 1/6 × ( 1 + f(E2) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E2) = 1/6 × ( 1 + f(E3) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E2) = 1/6 × ( 1 + f(E3) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E3) = 1/6 × ( 1 + f(E4) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E3) = 1/6 × ( 1 + f(E4) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E4) = 1/6 × ( 1 + f(E5) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) )
: f(E4) = 1/6 × ( 1 + f(E5) ) + 1/6 × ( 1 + f(E1) ) + 4/6 × ( 1 + f(E0) ) : f(E5) = 1/6 × 1 + 5/6 × ( 1 + f(E0) )
: f(E5) = 1/6 × 1 + 5/6 × ( 1 + f(E0) )よって、
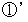 : f(E0) = f(E1) + 6 ・・・
: f(E0) = f(E1) + 6 ・・・ 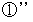
 : 4f(E0) - 5f(E1) + f(E2) + 6 = 0
: 4f(E0) - 5f(E1) + f(E2) + 6 = 0 : 4f(E0) + f(E1) - 6f(E2) + f(E3) + 6 = 0
: 4f(E0) + f(E1) - 6f(E2) + f(E3) + 6 = 0 : 4f(E0) + f(E1) - 6f(E3) + f(E4) + 6 = 0
: 4f(E0) + f(E1) - 6f(E3) + f(E4) + 6 = 0 : 4f(E0) + f(E1) - 6f(E4) + f(E5) + 6 = 0
: 4f(E0) + f(E1) - 6f(E4) + f(E5) + 6 = 0 : 5f(E0) - 6f(E5) + 6 = 0
: 5f(E0) - 6f(E5) + 6 = 0 →
→  にて、
にて、f(E2) = f(E1) - 30 ・・・
 &
&  →
→  にて、
にて、f(E3) = f(E1) - 210 ・・・
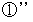 &
& 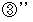 →
→ 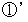 にて、
にて、f(E4) = f(E1) - 1290 ・・・ ④”
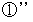 & ④”→
& ④”→ 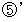 にて、
にて、f(E5) = f(E1) - 7770 ・・・

 &
&  →
→ 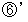 にて、
にて、f(E1) = 46656 ・・・ ⑥”
⑥” →
 にて、
にて、f(E0) = 46662
したがって答えは、 46662 回
※ 【 問 題 1 】の答えと微妙に異なります。
 確率 へ戻る
確率 へ戻る