(1) 調査による確率の変動 と 条件付き確率
-
赤玉3個と白玉3個が入っている袋があります。 眼をつぶったまま袋から1個を取り出して箱の中に入れます。 この時点で、 箱の中に赤玉が存在する確率は
では、 調査を開始します。 袋の中から無作為に3個玉を取り出します。 すると、 白玉が2個と赤玉が1個でした。 この時点で、 箱の中に赤玉が存在する確率はいくらでしょうか?
「 箱の中に赤玉が存在する確率は相変わらず
もし箱の中に赤玉が存在すると仮定すると、 そのときに袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個である確率は、 10通りのうちの6通りで 5分の3 です。 もし箱の中に白玉が存在すると仮定すると、 そのときに袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個である確率は、 10通りのうちの3通りで 10分の3 です。
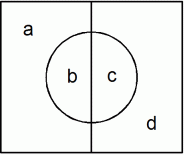
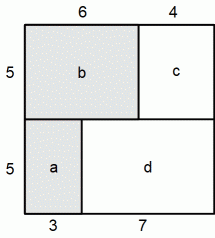
b : 箱の中に赤玉が存在し、かつ、袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個である確率
c : 箱の中に赤玉が存在し、かつ、袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個でない確率
a : 箱の中に白玉が存在し、かつ、袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個である確率
d : 箱の中に白玉が存在し、かつ、袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個でない確率
袋の中から無作為に3個玉を取り出したときに白玉が2個と赤玉が1個であったとき、 箱の中に赤玉が存在する確率は、 次のようになります。
以上より、 調査によって、 箱の中に赤玉が存在する確率は、
ついでに、 条件付き確率が成り立っているかどうか確かめてみましょう。
条件付き確率とは、 「 A → B の2つの時系的事象について、 2つの事象が共に発生する確率 を Bの事象が発生する確率 で割れば、 Bの事象が発生したことが公表された時点でのAの事象が発生していた確率が解る。」 という定理です。
このケースで 「 2つの事象が共に発生する確率 」 は b であり、 「 Bの事象が発生する確率 」 は a+b ですので、 上の式と同じになります。
(2) 無作為的残り物調査による確率の変動
モンティホール問題は 「 作為的残り物調査による確率の不動 」 の例です。 司会者は3枚のカードのうち1つの当たりカードがどれなのかを知っています。 最初に回答者が1枚のカードを手にしたとき、 回答者が手にしたカードが当たりである確率は 3分の1 で、 司会者が手にした2枚のカードのうちひとつが当たる確率は 3分の2 です。 その後、 司会者は2枚のうちの当たりでない方のカードを意図的に選んで公表して捨てるのですから、 司会者が最後に手にしているカードは 3分の2 の確率で当たりになっています。 司会者の当たる確率は、 司会者の作為的残り物調査によっても変動しないのです。
これに対して、 次のような問題は 「 無作為的残り物調査による確率の変動 」 をきたします。
赤、 青、 黄 のカードが6枚ずつあります。 裏返すとこれらのカードは白で区別がつきません。 よくきった後、 机の上に裏返しにして重ねて置きます。 次に一番上のカード ( 1枚目とする ) をめくらないで他の場所に移動させます。 その次に2枚目から11枚目をめくって机の上に散らばらします。 すると、 黄は2枚だけでした。 では、 1枚目のカードが黄である確率はいくらでしょうか?
答えは 3分の1 ではありません。 確かに 「 無作為的残り物調査 」 が行われる前は 3分の1 でしたが ・ ・ ・。 答えは簡単です、 無作為的残り物調査をされたカードを除外して考えればいいだけです。
答えは、 ( 3×6−10 ) 分 の ( 6−2 ) = 2分の1 です。
この問題を条件付き確率を使って解こうとすると、 少しややこしくなります。 でも、 やってみましょう。
-
1枚目のカードが黄で、 かつ、 2枚目から11枚目が結果どおりになる確率は、
1枚目のカードが黄以外で、かつ、2枚目から11枚目が結果どおりになる確率は、
したがって、 求める確率は、
シミュレーション :
赤、 青、 黄、 それぞれ6枚ずつある。 1枚選ぶ。
その後10枚選んだときに、 黄2枚だった。
最初に選んだのが黄である確率は? ( 1万回試行 )
プログラムの内容:
 確率 へ戻る
確率 へ戻る