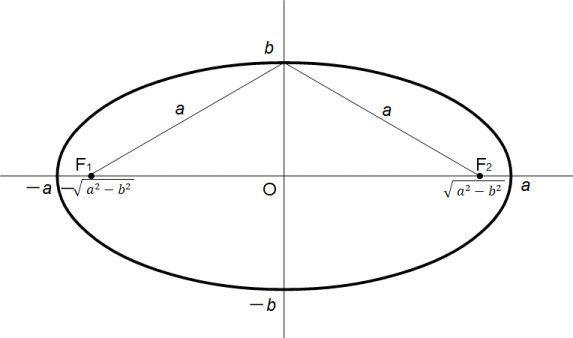
楕円の方程式：
　　　
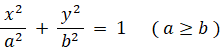
楕円の焦点：
　　　
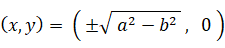
楕円の離心率：
　　　
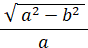
楕円の扁平率：
　　　

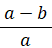
楕円の面積については、解析学 ＞ 楕円の面積を参照してください。

では、楕円の焦点を通る長軸に垂直な直線で区切られた外側の面積を求めてみましょう。
　　　

　　　
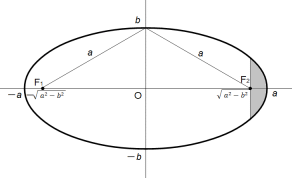
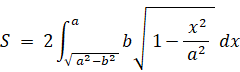
　　　次のように置きます。
　　　　　
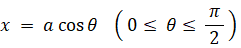
　　　すると、
　　　　　
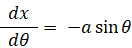
　　　よって、
　　　　　
　　　　　　
　　　　　　
　　　　　　
　　　　　　

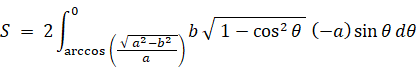
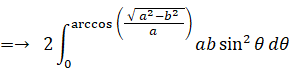
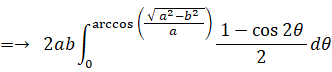
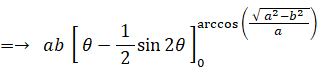
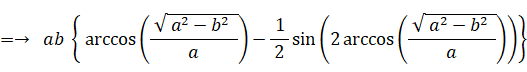
さて、地球の公転軌道 (楕円) の長径と短径の比は 1 ： 0.99986 です。
したがって、地球の公転軌道 (楕円) の離心率はおよそ 0.01673 です。
上の図を地球に当てはめてグレイの部分の面積が全体に占める割合を求めると、約 48.9 % になります。
この値は、次の十進BASIC のプログラムで求めました。
　　LET a = 100000
　　LET b = 99986
　　LET q = SQR(a^2-b^2)/a
　　PRINT "離心率(%) ＝ ";100*q
　　PRINT
　　LET e = ACOS(q)
　　LET s1 = PI * a * b
　　LET s2 = a*b*( e - SIN(2*e)/2 )
　　LET hi = s2 / s1
　　PRINT "全体に対する部分の面積の占める割合："
　　PRINT "　　　";hi
　　PRINT
　　PRINT "183/365 ＝ ";183/365
　　PRINT "182/365 ＝ ";182/365
　　PRINT "181/365 ＝ ";181/365
　　PRINT "180/365 ＝ ";180/365
　　PRINT "179/365 ＝ ";179/365;"　← 最も近い"
　　PRINT "178/365 ＝ ";178/365
　　PRINT "177/365 ＝ ";177/365
　　PRINT
　　END

※ 参照： ばいおりんの日常的物理学文集 ＞ 天文学と物理学 ＞ 冬至から夏至までの期間は夏至から冬至までの期間よりも短い