断面係数 も 断面二次モーメント も、 共に、 屈曲力が加えられたときの、 垂直応力の生じにくさを表す指標です。 円柱物質や直方体物質の屈曲時の垂直応力は、 曲がりの方向に垂直な 縦中心軸を含む縦断面 に対して対称的な点では、 向きが逆で大きさが等しくなります。 また、 垂直応力は、 その縦断面から遠い所ほど大きくなっています。 垂直応力の生じにくさとは、 曲げに対する「 形状的耐性 」 であると考えてよいと思います。 そしてこの２つには、 次のような関係があります。

　　　　


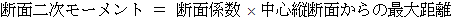
　 空中に寝かせた円柱物質の両端に屈曲力を作用させた場合、 曲がりの方向に垂直な 円柱の縦中心軸を含む縦断面 からの距離を 、 円柱の長さを 、 円柱の底面の直径を 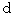、 両端に同じ向きに作用する屈曲力の大きさを 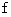とすると、 次のようになります。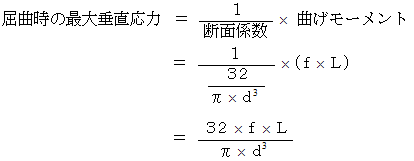

　　　　

　　　　

　 以上より、 円柱物質の曲げに対する抵抗力は、 直径の３乗に比例することが解ります。 垂直応力を小さくしようとする因子は、 曲げに対する形状的耐性を大きくしようとする因子だからです。


　 空中に寝かせた直方体物質の両端に屈曲力を作用させた場合、 曲がりの方向に垂直な 直方体の縦中心軸を含む縦断面 からの距離を 、 直方体の長さを 、直方体の底面の縦の長さを 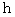、直方体の底面の横の長さを 、両端に底面の縦方向に作用する屈曲力の大きさを 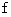とすると、 次のようになります。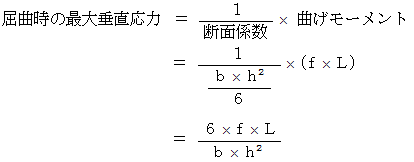

　　　　

　　　　

　 以上より、 直方体物質の曲げに対する形状的耐性は、 底面の縦幅の２乗と底面の横幅に比例することが解ります。 曲げに対する質的耐性は素材によって異なります。 したがって、 同じ素材の物質であれば、 底面の長方形の長い方の辺を屈曲力の加わる方向に対して水平に使った方が、 曲げに対する抵抗力は強くなることが解ります。 また、 同じ素材の物質であれば、 重ねることによって見かけ的に底面の縦幅を２倍にして使用した場合は、 曲げに対する抵抗力は２倍になります。 しかし、 底面の縦幅を実際に２倍にしたものを使用すると、 曲げに対する抵抗力が４倍にもなります。 私はこの原理を「 架橋における重ね損の法則 」と言っています。