「一辺の長さが整数で表される正方形がある。一辺の長さを2乗した正方形の面積と元の正方形の面積を加えると 20 になる。元の正方形の一辺の長さを求めよ。」という問題を解けるようにしたのもデカルトです。
まず、未知数を x と置く代数の発明です。次に、累乗の記号を発明したのもデカルトです。さらに、次元の異なる数を加えることは禁忌であるとされていた古代ギリシャ以来の数学の掟を破ったのも彼です。たしかに次元の異なる面積と体積を加えることは禁忌です。しかし、それはあくまでも単位についてであり、数についてではありません。デカルトによって数学は「次元の束縛」から解放されたのです。
ちなみに、先ほどの問題の答えは 一辺の長さが 2 となります。
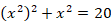
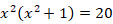
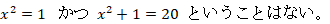
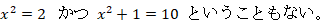
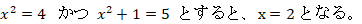
 数学と物理学 へ戻る
数学と物理学 へ戻る