音楽と物理学 へ戻る音名Ｃ を時計の12時の位置に配置したら、半音ずつ上がっていく音名を順に配置していき、 次のようにします。 音名時計の出来上がりです。 五度圏に似ていますが、 五度圏ではありません。
音名Ｃ から時計回りに「 アキストゼネコ 」と言いながら７つ移動してその音名をピックアップします。 ただし、 退場はさせません。 それからまた７つ移動してその音名をピックアップしていきます。 それから ・ ・ ・ ・ としていくと、 12個すべての音名をピックアップすることが出来て再び音名Ｃ に戻ってきます。 音名Ｃ から反時計回りに「 アキストゼネコ 」と言いながら７つ移動してその音名をピックアップします。 それからまた７つ移動してその音名をピックアップしていきます。 それから ・ ・ ・ ・ としていくと、 12個すべての音名をピックアップすることが出来て再び音名Ｃ に戻ってきます。
時計回りのときはシャープの付いている方の音名を選び、 反時計回りのときはフラットの付いている方の音名を選ぶことにして、 次のように並べます。 これは、 円になっている五度圏を時計の６時の位置で切って開いて直線化したものです。
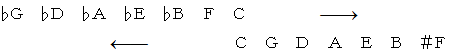
この音名たちの並びを 「 右に行くほど５度ずつ上がっている。」 と言います。
振動数の比が １：２ になっている音は同じ音名になります。 音名Ａ の振動数を
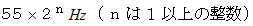とするとき、 振動数が 
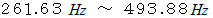の範囲における、 シャープやフラットが付いていない７つの音名について言うならば、 最も低い音の音名は Ｃ で、 最も高い音の音名は Ｂ で、 振動数の小さい順に並べると、 Ｃ Ｄ Ｅ Ｆ Ｇ Ａ Ｂ となります。これらの７つの音名のうちの２つの音名の音高の隔たりを表すのに「 度 」を使うことがあります。「 度 」は「 シャープやフラットが付いていない音名または階名の音高の段差 」に
を加えたものです。 たとえば、 Ｃ と Ｃ は １度、 Ｃ と Ｇ は ５度、 ド と ソ は ５度 になります。
を日本語に訳すと 
です。 Ｃ を主音とする長調（ ハ長調 ）は、 五線譜ではシャープもフラットも付きません。 主音がそれより ５度上がった長調（ ト長調 ）は、 五線譜ではシャープが１つ付きます。 さらに主音が ５度上がった長調（ 二長調 ）は、 五線譜ではシャープが２つ付きます。 Ｃ を主音とする長調（ ハ長調 ）より ５度下がった長調（ ヘ長調 ）は、 五線譜ではフラットが１つ付きます。 さらに主音が ５度下がった長調（ 変ロ長調 ）は、 五線譜ではフラットが２つ付きます。長調の Ⅳの和音 は、 その主音よりも ５度下がった音を主音とする長調の Ⅰの和音 に等しく、 長調の Ⅴの和音 は、 その主音よりも ５度上がった音を主音とする長調の Ⅰの和音 に等しくなっています。 したがって、 たとえば、 二長調で
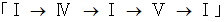の和音進行は、 和音コードで言うと 
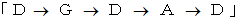になります。２つ以上の項目を円周上に等間隔で並べて、 定められた数だけ時計回りに移動して次々に項目をピックアップしていくときに、 すべての項目をピックアップできるのは次のような場合です。
１つずつ移動するとき。 項目数よりも１つ少ない数ずつ移動するとき。 項目数よりも１つ少ない数を割り切れる数ずつ移動するとき。 項目数が奇数であり、 項目数に を加えた数の半分の数ずつ移動するとき。 項目数が奇数であり、 項目数に を加えた数の半分の数を割り切れる数ずつ移動するとき。
項目数が４の倍数であり、 項目数の半分に を加えた数ずつ移動するとき。 項目数が４の倍数であり、 項目数の半分に を加えた数を割り切れる数ずつ移動するとき。
音名時計からすべての音名をピックアップすることが出来たのは、 下から２番目の条件に当てはまったからです。 これをもう少し数学的に考えますと、「 ７ の １ から 12 倍 までの倍数を 12 で割った余りが、 すべて異なるからだ。」ということになります。 それは、 12 と ７ が互いに素になっているためです。 要するに、「 回転総取得条件は、 総数と回転数が互いに素であることである。」 ということになります。
７ ÷ 12 ＝ ０ 余り ７
14 ÷ 12 ＝ １ 余り ２
21 ÷ 12 ＝ １ 余り ９
28 ÷ 12 ＝ ２ 余り ４
35 ÷ 12 ＝ ２ 余り 11
42 ÷ 12 ＝ ３ 余り ６
49 ÷ 12 ＝ ４ 余り １
56 ÷ 12 ＝ ４ 余り ８
63 ÷ 12 ＝ ５ 余り ３
70 ÷ 12 ＝ ５ 余り 10
77 ÷ 12 ＝ ６ 余り ５
84 ÷ 12 ＝ ７ 余り ０
（ 証 明 ）
０ ＜ ｎ ＜ ｍ ＜ 13 を満たす整数 ｎ と ｍ について、 ７ｎ と ７ｍ を 12 で割った余りが等しいと仮定する。
すると、
７ｍ － ７ｎ は 12 で割り切れる。
つまり、 ７ （ ｍ － ｎ ） は 12 で割り切れる。
ところが、 ７ と 12 は互いに素であり、 かつ、 ｍ － ｎ は12未満の自然数なので、 ７ （ ｍ － ｎ ） は 12 で割り切れない。 これは、 仮定から導き出された結果と矛盾している。 よって、 仮定は間違いである。
したがって、 ７ の １ から 12 倍 までの倍数を 12 で割った余りは、 すべて異なる。
f (x) を x に作用して x を 12 で割った余りを出力する演算子とすると、 次の２つが成り立ちます。
f (x) ＝ f ( x + 12k ) （ k は整数 ）
０ ≦ x ＜ 12 のとき f (x) ＝ x
x ＝ －７ ０ ７ 14 21 28 35
f (x) ＝ ５ ０ ７ ２ ９ ４ 11
ファ ド ソ レ ラ ミ シ
x ＝ －28 －21 －14 42 49 56
f (x) ＝ ８ ３ 10 ６ １ ８
♭ラ ♭ミ ♭シ ♯ファ ♯ド ♯ソ
♭ラ ♭ミ ♭シ
長調 ： ドレミファソラシド の ３ ６ ７（ ミ ラ シ ）を半音下げると短調になります。
♯ファ ♯ド ♯ソ
短調 ： ラシドレミファソラ の ３ ６ ７（ ド ファ ソ ）を半音上げると長調になります。
f (x) ＝ f ( x + 12k ) （ k は整数 ） ０ ≦ x ＜ 12 のとき f (x) ＝ xx ＝ －７ ０ ７ 14 21 28 35
f (x) ＝ ５ ０ ７ ２ ９ ４ 11
ファ ド ソ レ ラ ミ シ
x ＝ －28 －21 －14 42 49 56
f (x) ＝ ８ ３ 10 ６ １ ８
♭ラ ♭ミ ♭シ ♯ファ ♯ド ♯ソ
♭ラ ♭ミ ♭シ
長調 ： ドレミファソラシド の ３ ６ ７（ ミ ラ シ ）を半音下げると短調になります。
♯ファ ♯ド ♯ソ
短調 ： ラシドレミファソラ の ３ ６ ７（ ド ファ ソ ）を半音上げると長調になります。