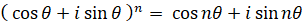�@ は ド・モアブル の定理 です。今からこの式を証明します。

n ＝ 1 のとき、明らかに �@ は成り立つ。
n ＝ k のとき、�@ が成り立つと仮定する。つまり、次の式が成り立つと仮定する。
　　　
ところで、
　　　
　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　
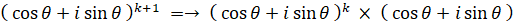
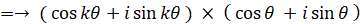
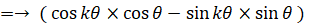
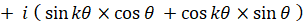
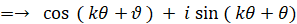
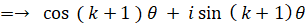
　というわけで、n ＝ k のとき �@ が成り立つと仮定すると、n ＝ k＋1 のときも �@ が成り立つことが分かった。したがって、数学的帰納法により、すべての自然数 n について �@ が成り立つことが分かる。

ド・モアブル の定理 は、大きさが 1 の複素数の累乗を表します。複素数の n 乗は次の式で表されます。
　　　( e ^iθ ) ⁿ　＝ e ^inθ