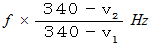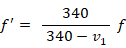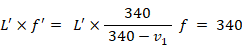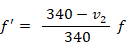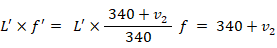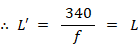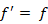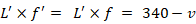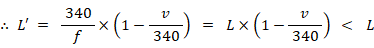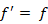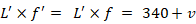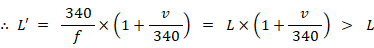数直線上の原点に音源があり、正の方向に観察者がいます。正の方向への移動の速さはプラスで表し、負の方向への移動の速さはマイナスで表すことにします。音速を 340 とし、風に対する音源の速さを
v1 、風に対する観察者の速さを
v2 で表します。こういう設定にしたのは、無風という条件にするためです。なお、
v1 も
v2 も 170 未満とします。音源が出す音の振動数を
f で表します。このとき観察者が聞く音の振動数は次のようになります。これはドップラー効果と言われます。
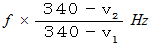
無風下で音源も観察者も移動しない場合の振動数
f の音の波長を
L で表します。すると次の式が成り立ちます。
L ×
f = 340
ではこれから、次のようないろんなケースで、観察者が観察する音の波長はどのように変化するのか見てみましょう。なお、音の高さは波長ではなく振動数で表されます。
① 音源が移動して観察者に近づく ( 音速変化なし )
② 観察者が移動して観察者に近づく ( 音速変化あり )
③ 音源と観察者が正の方向に同じ速さで移動する ( 音速変化あり )
④ 音源と観察者が負の方向に同じ速さで移動する ( 音速変化あり )
※ 参考:
基礎物理学 > 音速と音高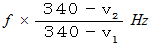
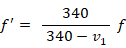
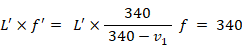

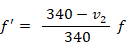
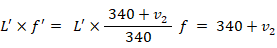
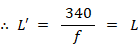
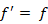
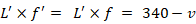
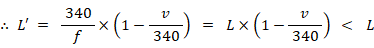
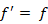
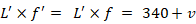
 基礎物理学 へ戻る
基礎物理学 へ戻る 大学生のための物理学 へ戻る
大学生のための物理学 へ戻る