数学と物理学 へ戻る
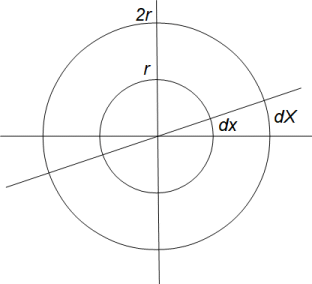
半径 r の円Ａの円周上の無数の点は、大きさが０で、隣同士の距離は０よりもわずかに大きいです。その距離を dx とします。
半径 2r の円Ｂの円周上の無数の点は、大きさが０で、隣同士の距離は０よりもわずかに大きいです。その距離を dX とします。
dx と dX との間には次のような関係があります。
dX ＝ 2dx ・・・ C
円Ａ と 円Ｂ の円周上の無数の点にはすべて１という数が割り当てられています。それを円周に沿って積分すると円周の長さになります。
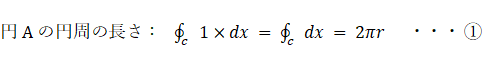
C を A の左辺 に代入し、さらに @ を代入すると、
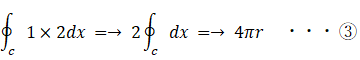
辻褄が合っています。
中心が同じ位置にあって半径の異なる２つの円周上の点は １：１ 対応していますが、その間隔が異なるために円周の長さが異なるのです。
円筒のシリンダーの中にピストンが隙間なく納められていてスムースにスライドするためには、設計図では表すことのできないわずかな隙間（ 遊び ）が必要です。遊びを作るには人間の高度な技術（ 職人技 ）を必要とします。シリンダーの中でピストンを回転してみてください。ピストンの外周上の点が通るシリンダー内部の円軌道について、シリンダー内部の円周が、ピストンの外周よりもわずかに長くなっています。このことによって生じるわずかな滑りが理想的なピストン運動を生むのです。
音楽も言葉も同じです。間 や 行間 が大切なのです。
参考： その他の数学 ＞ アリストテレスの輪のパラドックス
【 反 論 】
-
（１） 重心から辺上の点への位置ベクトルを方向を変えずに大きさを２倍にしてできる図形についても、以上と同じ発想ができます。しかし、辺の長さが２倍になったからといって辺上の隣り合う２点の間隔が２倍になると考えるのは間違いではないでしょうか？ 辺の長さが２倍になっても辺上の隣り合う２点の間隔は同じだと思います。
（２） 大きさが０の点を無数に一列に並べると直線ができます。 0×∞ ＝ 0 なので、隣り合う２点の間にわずかな隙間がなければならないとの考えは間違っています。 0×∞ ＝ 0 とは限りません。不定形です。 h が限りなく０に近づくとき、1/h ＝ ∞ ですので、 h が限りなく０に近づくとき、 1 ＝ h × 1/h ＝ 0×∞ になるではないですか。その上、「実数の連続性」や「一変数実関数の連続性」という概念があるではないですか。
-
（１） ２つの相似な図形で、対応する辺の長さの比が１：２の場合、重心を重ね対応する辺が平行になるようにしてから、重心から大きな図形の辺上のある点に直線分を引くと、必ず小さな図形の辺上の１点に交わり、この２つの点たちの対応を考えると、小さな図形の辺上の点と大きな図形の辺上の点とはすべて１：１対応になります。ということは、辺の長さが２倍になれば辺上の隣り合う２点の間隔は２倍になると考えるのは間違いではないと思います。
（２） ０〜１の間で無作為に実数を１つ抽出するとき、0.45〜0.55 の範囲に入っている確率は 0.1 ですが、0.5 である確率は 0 です。というわけで、点の大きさは限りなく０に近いのではなく０です。ですから、0×∞ ＝ 0 だと思います。したがって、隣り合う２点の間隔は０ではなく、隣り合う２点の間には限りなく０に近いのですがわずかな隙間があるのです。
-
点の大きさは、限りなく０に近い？ それとも０？
参考：
1 − 0.9999999・・・ ＝ 0
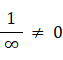
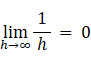
1 m の線分 も 無限長の直線 もそれを構成する点の数は同じである。
↓
したがって、隣り合う２点の間にはわずかな隙間があるはずだ。
※ 参照： 大学生のための数学 ＞ 解析学 ＞ スカラー場の線積分のイメージ
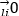と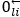 
という記号を作り、次のように定義します。-
限りなく０に近い負の数：
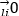
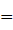
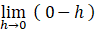
限りなく０に近い正の数：
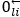
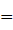
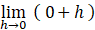
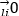や 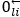では割ることができ、 a ＞ 0 のとき、 a を 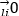で割ると −∞ になり、 a を 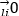で割ると ＋∞ になります。点の大きさは？ 0 または
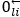のどちらかと思うのですが、どちらなのでしょう？ 今の私には分かりません。ただし、線上の隣り合う２点間の距離は 0 でなくて 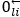だと思います。なぜなら、もし 0 ならば２点は重なって同一点になってしまうからです。※ 参照： 大学生のための数学 ＞ 論理学 ＞ 幾何学における集合の濃度の比較
ちなみに、今回述べた隣どうしの数の隙間の問題 は 関数の連続性 とは全く異なる概念であり、隣どうしの数の隙間があるからといって関数の連続性が否定されるわけではありません。