(1) 永久にチャレンジしても1回も当たりが出ない確率
-
何度引いても同じ確率で当たりが出るくじがある。
何回チャレンジする? → n 回
1回のチャレンジで当たりが出る確率は 1 / n である。
n 回チャレンジして1回も当たりが出ない確率は次の式で与えられる。
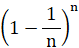
果てしなくチャレンジしたときに1回も当たりが出ない確率は次の式で与えられる。
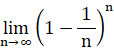
この式は、次の2通りに変形することができる。
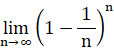
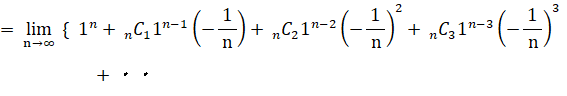
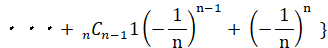
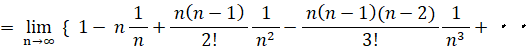
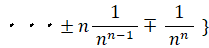
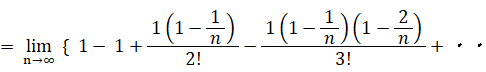
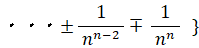
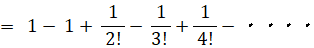
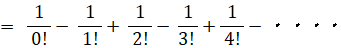
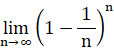
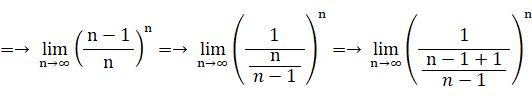
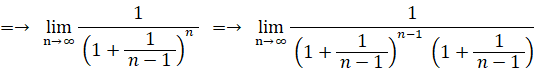
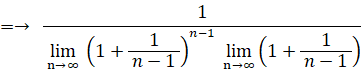
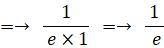
当たる確率が 1/n ( n は無限大の自然数 ) のくじを繰り返し n 回引いたとき、一度も当たらない確率は 1/e であることを証明してみましょう。
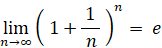
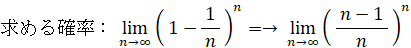
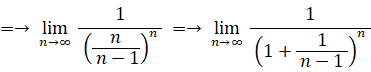
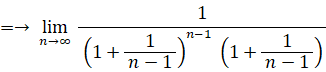
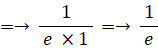
(2) 無数の人たちによる集団プレゼント交換会
-
そのルール:
1人が1個のプレゼントを用意して集まる。
集まったプレゼントの中から1人1個のプレゼントがもらえる。
プレゼンをもらったらすぐにそのプレゼントを持って帰らなければならない。
プレゼントは1人ずつ順番にもらえる。
そのもらい方は、余ったプレゼントの中から無作為に1個を抽出することによる。
プレゼントをもらえるのは直前に自分が用意したプレゼントが抽出された人である。
もし、それに該当する者がない場合は、最も年上の人になる。
1人も自分が用意したプレゼントに当たらない確率を求めてみよう。
まず、無数の人たちではなく、n 人の人たちによる集団プレゼント交換会において、1人も自分が用意したプレゼントに当たらない確率を Pn とする。
n 人の人たちによる集団プレゼント交換会において、1人も自分が用意したプレゼントに当たらない場合の数を A n とすると、Pn と A n の関係は次のようになる。
Pn = A n / n! よって、 A n = n! Pn
① 最初にプレゼントをもらった人と2番目にプレゼントをもらった人がプレゼントの互換になっている場合の数
A n-2 × ( n-1 )
※ n-1 は、最初の人が自分が用意したプレゼント以外のものを1つゲットする場合の数
※ 最初の人以降は自分が用意したプレゼント以外の物をゲットするのであるが、
その場合の数が A n である。
※ 最初の人は自分が用意したプレゼント以外の物をゲットするのである。
② 最初にプレゼントをもらった人と2番目にプレゼントをもらった人がプレゼントの互換になっていない場合の数
A n-1 × ( n-1 )
※ 2番目の人以降は自分が用意したプレゼント以外の物をゲットするのであるが、
その場合の数が A n-1 である。
※ 2番目の人は自分が用意したプレゼントと最初の人が用意したプレゼント以外
の物をゲットするのであるが、 自分が用意したプレゼントはもう無いので、
最初の人が用意したプレゼント以外の物をゲットするのである。
① と ② より、次の漸化式ができる。
A n = ( n-1 ) × ( A n-1 + A n-2 )
したがって、
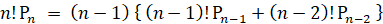
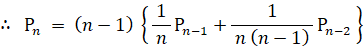
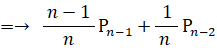
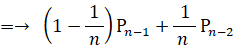
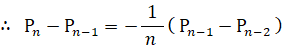
ここで、
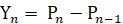 と置くと、
と置くと、
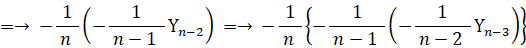
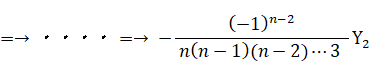
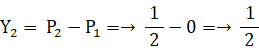 だから、
だから、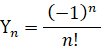
つまり、
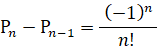
よって、
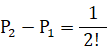
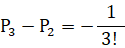
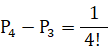
・
・
・

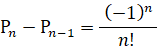
これらを辺々加えて、
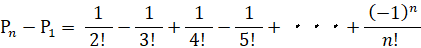
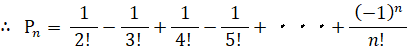
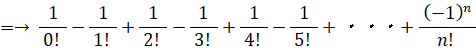
したがって、
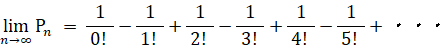
よって、
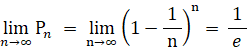
 確率 へ戻る
確率 へ戻る