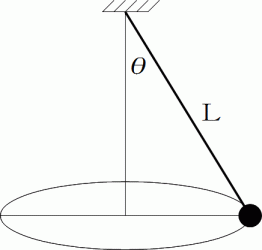
円錐振り子では、 重りは等速円運動をしますが、 重りの回転速度 （ 角速度 ） が大きくなるとそれに伴って軌道半径が大きくなります。 重りの質量を 、 紐の長さを 、 張力の大きさを とします。 上の図より、 次の式が成り立っていることがわかります。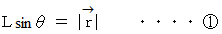
　　　　　

　 運動方程式（ 接法ベクトル表示 ）は次のように表されます。 右辺は速度の向きの変化の原動力となる 向心力 を表しています。 接線方向の力は ０ なので、 速度の大きさは変化しません。
　　　　　

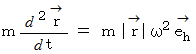
したがって、 次の式が成り立ちます。
　　　　　

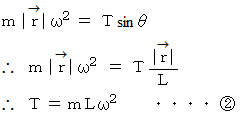
一方、 鉛直方向の力のつり合いより、 次の式が成り立ちます。
　　　　　

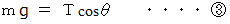
と より、 次の式が成り立ちます。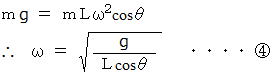
　　　　　
　　　　　
と より、 次の式が成り立ちます。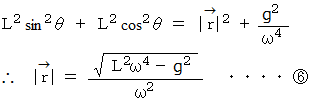
　　　　　
　 求めたかったのは、 と です。 はピンときませんが、 を見ると、 が大きいほど （ 重りの回転移動角速度 ）が大きくなりますので、 軌道半径が大きいほど が大きくなることがわかります。 逆に言うと、 が大きいほど軌道半径が大きくなるということです。