【 問 題 】
-
x y z の3次元直交座標系を考えてください。
x z 平面上の原点を中心とする半径1の円を z 軸を回転軸として x 軸から y 軸の方向に時刻 0 〜 t の間一定の速さで180度回転させます。
x y 平面上の原点を中心とする半径1の円を x 軸を回転軸として y 軸から z 軸の方向に時刻 0 〜 t の間一定の速さで180度回転させます。
このとき2つの円の交点が x 軸と z 軸の正の範囲に描く軌道を表すベクトルを示してください。
-
x z 平面上の原点を中心とする半径1の円の方程式 :
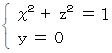
この円を z 軸を回転軸として θ ラジアン回転した円は次の位置ベクトルで表される。

x y 平面上の原点を中心とする半径1の円の方程式 :
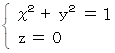
この円を x 軸を回転軸として θ ラジアン回転した円は次の位置ベクトルで表される。
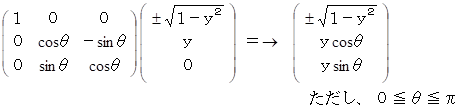
次の連立方程式を立てて解く
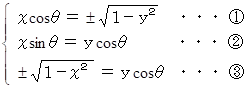
 より、
より、 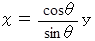
これを
 に代入して、
に代入して、 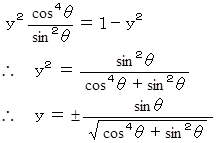
したがって、
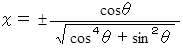
したがって、
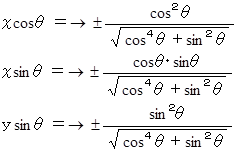
したがって、 交点が描く軌道を表すベクトルは次のように表される。
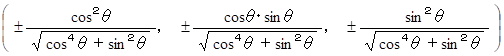
問題は x 軸と z 軸の正の範囲に描く軌道を表すベクトルなので、 答えは次のようになる。
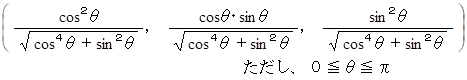
 ベクトル解析 へ戻る
ベクトル解析 へ戻る