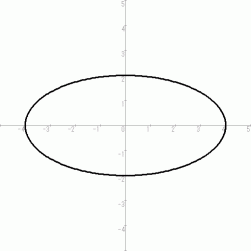
上図のような楕円があります。 短軸と長軸の長さの比は １：２ です。x 軸よりも上の部分 と y 軸よりも右の部分 は、 それぞれ次のようになります。
　　　　　　　
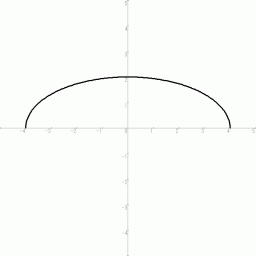
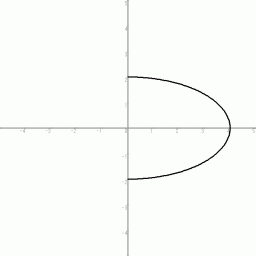
　 これらの面積は等しくなっています。 さて、 前者を x 軸の周りに360度回転してできる楕円球の体積 と 後者を y 軸の周りに360度回転してできる楕円球の体積 を比較してみましょう。 「 同じ面積のものを重なりなく１回転させてできる回転体なのだから、 体積は当然等しくなる。」 と考えてしまいそうになりますが、 実際は後者の体積の方が２倍大きくなります。 それは、 回転体を上から （ z 軸の方から ） 眺めた図をイメージすると解ると思います。


　 楕円の方程式 ：
　　　　　
　 これを x 軸の周りに360度回転してできる楕円球の体積は、 次のようになります。
　　　　　
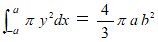
　 これを y 軸の周りに360度回転してできる楕円球の体積は、 次のようになります。
　　　　　
　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　

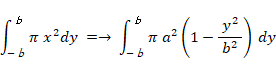
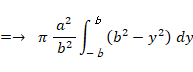
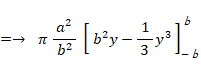
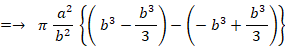
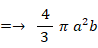
　 回転体の体積を求める方法については、　解析学 ＞ 球の部分の体積や面積や立体角　をご覧ください。