ピタゴラスは、ド と ド の振動数比が 1:2 で、ド と ソ の振動数比が 2:3 であることから、次のようにして 12個の音を作りました。
(3/2)12 × (1/2)6 ≒→ 2.02728652954102 ≒→ 2
1 ≦ (3/2)n × (1/2)m ≦ 2 ( n は −5 〜 6 の整数 m は −3 〜 3 の整数 )
上の式は次のように解釈できます。
3n ( n は −5 〜 6 の整数 )
これに 2m( m は整数 )をかけて 1 以上 2 以下 の数にする。
こうして出来上がったのがピタゴラス音律ですが、西洋音楽界では 1600 年代になってからこれに代わる音律がいろいろと登場してきます。純正調や平均律などです。そして、 1850 年頃からは平均律が主体になります。
さて、天才数学者オイラーが活躍したのは 1725 年頃からの半世紀です。彼はピタゴラス音律に習って純正調の振動数を次のように解析しました。
3n5m ( n と m は整数 )
これに 2k( k は整数 )をかけて 1 以上 2 以下 の数にする。
では、彼の思考の跡を想像してみましょう。
純正調の基本は ド:ミ:ソ = 4:5:6 の和音の振動数比です。
↓
2オクターブ高いミ と 1オクターブ高いソ に置き換えます。
↓
ド:ミ:ソ = 4:20:12 =→ 1:5:3 の和音の振動数比になります。
↓
3n5m ( n や m は整数 )の音を作っていきます。
| 3 | |||||||
|---|---|---|---|---|---|---|---|
| −2乗 | −1乗 | 0乗 | 1乗 | 2乗 | |||
| 5 | −2乗 | ♭ファ | ♭ド | ♭ソ | |||
| −1乗 | ♭レ | ♭ラ | ♭ミ | ♭シ | |||
| 0乗 | ファ | ド | ソ | レ | |||
| 1乗 | ラ | ミ | シ | ||||
| 2乗 | #ファ | #ド | #ソ | #レ | |||
| 3乗 | #ラ | #ミ | #シ | ||||
( 十進BASIC プログラム )
PRINT " 2^k 3^n 5^m"
FOR n=-2 TO 2
FOR m=-2 TO 3
FOR k=-6 TO 5
LET Q = 2^k * 3^n * 5^m
IF Q =>1 AND Q =<2 THEN
PRINT " ";k;" ";n;" ";m;" ";Q
END IF
NEXT k
NEXT m
NEXT n
END
( 実行結果 )
2^k 3^n 5^m
4 -2 0 1.77777777777778 ×
1 -2 1 1.11111111111111 ×
-1 -2 2 1.38888888888889 #ファ
-3 -2 3 1.73611111111111 #ラ
4 -1 -1 1.06666666666667 ♭レ
2 -1 0 1.33333333333333 ファ
0 -1 1 1.66666666666667 ラ
-3 -1 2 1.04166666666667 #ド
-5 -1 3 1.30208333333333 (#ミ)
5 0 -2 1.28 (♭ファ)
3 0 -1 1.6 ♭ラ
0 0 0 1 ド
1 0 0 2 ド
-2 0 1 1.25 ミ
-4 0 2 1.5625 #ソ
-6 0 3 1.953125 (#シ)
4 1 -2 1.92 (♭ド)
1 1 -1 1.2 ♭ミ
-1 1 0 1.5 ソ
-3 1 1 1.875 シ
-6 1 2 1.171875 #レ
2 2 -2 1.44 ♭ソ
0 2 -1 1.8 ♭シ
-3 2 0 1.125 レ
-5 2 1 1.40625 ×
表の中の音に 2k( k は整数 )をかけて振動数比を1 以上 2 以下にします。
#ド #レ #ミ #ファ #ソ #ラ #シ の振動数比( ドを1とする ):
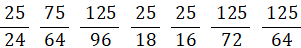
ド レ ミ ファ ソ ラ シ の振動数比( ドを1とする ):
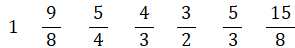
※ 純正調と全く同じです。
♭ド ♭レ ♭ミ ♭ファ ♭ソ ♭ラ ♭シ の振動数比( ドを1とする ):
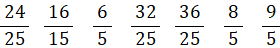
#ド 25/24 = 1.0416666666666・・・
#レ 75/64 = 1.171875
#ミ 125/96 = 1.3020833333333・・・
#ファ 25/18 = 1.3888888888888・・・
#ソ 25/16 = 1.5625
#ラ 125/72 = 1.7361111111111・・・
#シ 125/64 = 1.953125
ド 1
レ 9/8 = 1.125
ミ 5/4 = 1.25
ファ 4/3 = 1.3333333333333・・・
ソ 3/2 = 1.5
ラ 5/3 = 1.6666666666666・・・
シ 15/8 = 1.875
♭ド 24/25 = 0.96
♭レ 16/15 = 1.0666666666666・・・
♭ミ 6/5 = 1.2
♭ファ 32/25 = 1.28
♭ソ 36/25 = 1.44
♭ラ 8/5 = 1.6
♭シ 9/5 = 1.8
#レ 75/64 = 1.171875
#ミ 125/96 = 1.3020833333333・・・
#ファ 25/18 = 1.3888888888888・・・
#ソ 25/16 = 1.5625
#ラ 125/72 = 1.7361111111111・・・
#シ 125/64 = 1.953125
ド 1
レ 9/8 = 1.125
ミ 5/4 = 1.25
ファ 4/3 = 1.3333333333333・・・
ソ 3/2 = 1.5
ラ 5/3 = 1.6666666666666・・・
シ 15/8 = 1.875
♭ド 24/25 = 0.96
♭レ 16/15 = 1.0666666666666・・・
♭ミ 6/5 = 1.2
♭ファ 32/25 = 1.28
♭ソ 36/25 = 1.44
♭ラ 8/5 = 1.6
♭シ 9/5 = 1.8
半音違い:
-
ド:#ド = 1.000:1.042
レ:#レ = 1.125:1.172 =→ 1.000:1.042:
ミ:#ミ = 1.250:1.302 =→ 1.000:1.042:
ファ:#ファ = 1.333:1.389 =→ 1.000:1.042
ソ:#ソ = 1.500:1.563 =→ 1.000:1.042:
ラ:#ラ = 1.667:1.736 =→ 1.000:1.041:
シ:#シ = 1.875:1.953 =→ 1.000:1.042:
♭ド:ド = 0.960:1.000
♭レ:レ = 1.067:1.125 =→ 0.948:1.000
♭ミ:ミ = 1.200:1.250 =→ 0.960:1.000
♭ファ:ファ = 1.280:1.333 =→ 0.960:1.000
♭ソ:ソ = 1.440:1.500 =→ 0.960:1.000
♭ラ:ラ = 1.600:1.667 =→ 0.960:1.000
♭シ:シ = 1.800:1.875 =→ 0.960:1.000
-
#ミ:ファ = 1.302:1.333 =→ 1.000:1.024
ミ:♭ファ = 1.250:1.280 =→ 1.000:1.024
シ:♭ド = 1.875:1.920 =→ 1.000:1.024
#シ:ド = 1.953:2.000 =→ 1.000:1.024
#ド:♭レ = 1.042 :1.067 =→ 1.000:1.024
#レ:♭ミ = 1.172:1.200 =→ 1.000:1.024
#ファ :♭ソ = 1.389:1.440 =→ 1.000:1.037
#ソ:♭ラ = 1.563:1.600 =→ 1.000:1.024
#ラ:♭シ = 1.736:1.800 =→ 1.000:1.037
※ 1.024 = 128 / 125
 音楽と物理学 へ戻る
音楽と物理学 へ戻る